如图，抛物线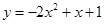
交y轴于点A，交x轴正半轴于点B．P为线段AB上一动点，作直线PC⊥PO，交过点B垂直于x轴的直线于点C．过P点作直线MN平行于x轴，交y轴于点M，交过点B垂直于x轴的直线于点N．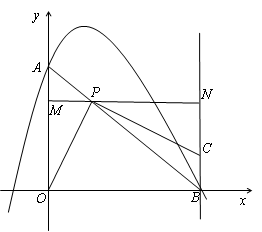
（1）求点A，B的坐标；
（2）证明：OP=PC
邻边不相等的平行四边形纸片，剪去一个菱形，余下一个四边形，称为第一次操作；在余下的四边形纸片中再剪去一个菱形，又余下一个四边形，称为第二次操作；……依次类推，若第n次操作余下的四边形是菱形，则称原平行四边形为n阶准菱形，如图1，平行四边形
中，若
，则平行四边形为1阶准菱形。
（1）判断与推理：
① 邻边长分别为2和3的平行四边形是__________阶准菱形；
② 小明为了剪去一个菱形，进行如下操作：如图2，把平行四边形沿着
折叠（点
在
上）使点
落在
边上的点
，得到四边形
，请证明四边形是菱形。
（2）操作、探究与计算：
① 已知平行四边形的邻边分别为1，
裁剪线的示意图，并在图形下方写出
的值；
② 已知平行四边形的邻边长分别为
，满足
，请写出平行四边形是几阶准菱形。
为了鼓励市民节约用水，某市居民生活用水按阶梯式水价计费。下表是该市民居民“一户一表”生活用水阶梯式计费价格表的部分信息：
（说明：①每户产生的污水量等于该户自来水用水量；②水费=自来水费用+污水处理费）
已知小王家2012年4月用水20吨，交水费66元，5月份用水25吨，交水费91元。
（1）求a，b的值；
（2）随着夏天的到来，用水量将增加。为了节省开支。小王计划把6月份的水费控制在不超过家庭月收入的2%，若小王家的月收入为9200元，则小王家6月份最多能用水多少吨？
如图，
中，
是它的角平分线，
，
在
边上，
为直径的半圆
经过点
，交
于点
。
（1）求证：
是
的切线；
（2）已知
，的半径为4，求图中阴影部分的面积。
某学校要求成立一支由6名女生组成的礼仪队，初三两个班各选6名女生，分别组成甲队和乙队参加选拔，每位女生的升高统计如下图，部分统计量如下表：
（1）求甲队身高的中位数；
（2）求乙队身高的平均数及身高不小于1.70米的频率；
（3）如果选拔的标准是身高越整齐越好，那么甲、乙两队中那一队将被录取？请说明理由。
如图，已知一次函数与反比例函数的图像交于点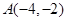
和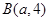
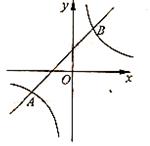
（1）求反比例函数的解析式和点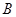
的坐标；
（2）根据图像回答，当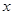
在什么范围内时，一次函数的值大于反比例函数的值？