（本小题满分14分）已知线性变换
是按逆时针方向旋转
的旋转变换，其对应的矩阵为
，线性变换
：
对应的矩阵为
．
（Ⅰ）写出矩阵、；
（Ⅱ）若直线
在矩阵
对应的变换作用下得到方程为
的直线，求直线的方程．
（本小题满分12分）已知函数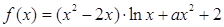
．
（Ⅰ）当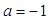
时，求
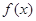在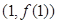
处的切线方程；
（Ⅱ）设函数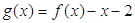
，
①若函数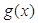
有且仅有一个零点时，求
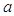的值；
②在①的条件下，若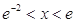
，
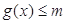，求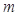
的取值范围。
（本小题满分12分）已知椭圆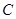
的中心在原点
，焦点在
轴上，离心率为
，右焦点到右顶点的距离为
（Ⅰ）求椭圆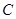的标准方程；
（Ⅱ）是否存在与椭圆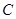交于
两点的直线
：
，
使得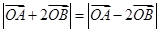
成立？若存在，求出实数
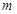的取值范围，若不存在，
请说明理由.
（本小题满分12分）设数列
的前
项和为
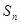，且满足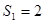
,
.
（Ⅰ）求通项公式
；
（Ⅱ）设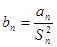
，求证：
．
（本小题满分12分）已知三棱柱
的侧棱垂直于底面，
，
，
，
，
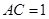分别是
，
的中点．
（Ⅰ）证明：
；
（Ⅱ）证明：
平面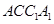
；
（Ⅲ）求二面角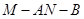
的余弦值．
（本小题满分12分） 在△ABC中，角A，B，C对边分别为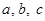
满足：
，
（Ⅰ）求角A 的大小；
（Ⅱ）求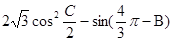
的最大值，并求取得最大值时角B，C的大小.