已知函数 ,
,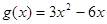 ,又函数
,又函数 在
在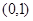 单调递减,而在
单调递减,而在 单调递增.
单调递增.
(1)求 的值;
的值;
(2)求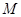 的最小值,使对
的最小值,使对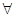
 ,有
,有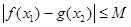 成立;
成立;
(3)是否存在正实数 ,使得
,使得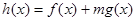 在
在 上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.
上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.
如图,椭圆的中心为原点 ,离心率 ,一条准线的方程是

(Ⅰ)求椭圆的标准方程;
(Ⅱ)设动点
满足:
,其中
、
椭圆上的点,直线
与
的斜率之积为
,
问:是否存在定点
,使得
与点
到直线
:
的距离之比为定值;若存在,求
的坐标,若不存在,说明理由.
如图,在四面体
中,平面
⊥平面
,
,
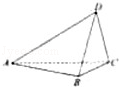
(Ⅰ)求四面体
的体积;
(Ⅱ)求二面角
的平面角的正切值.
设
的导数为
,若函数
的图象关于直线
对称,且
.
(Ⅰ)求实数
的值
(Ⅱ)求函数
的极值.
设函数 .
(1)求
的最小正周期;
(2)若函数
的图象按
平移后得到的函数
的图象,求
在
上的最大值.
某市公租房的房源位于
个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,求该市的4位申请人中:
(I)没有人申请
片区房源的概率;
(II)每个片区的房源都有人申请的概率.