(本小题满分12分)某中学刚搬迁到新校区,学校考虑,若非住校生上学路上单程所需时间人均超过20分钟,则学校推迟5分钟上课.为此,校方随机抽取100个非住校生,调查其上学路上单程所需时间(单位:分钟),根据所得数据绘制成如下频率分布直方图,其中时间分组为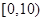 ,
,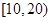 ,
,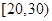 ,
,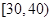 ,
,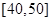 .
.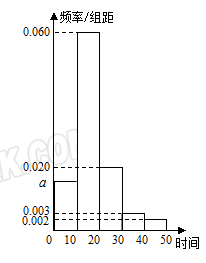
(1)求频率分布直方图中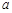 的值;
的值;
(2)从统计学的角度说明学校是否需要推迟5分钟上课;
(3)若从样本单程时间不小于30分钟的学生中,随机抽取2人,求恰有一个学生的单程时间落在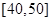 上的概率.
上的概率.
(本小题共12分)
已知△ABC的角A,B,C的对边依次为a,b,c,若满足 ,
,
(1)求∠C大小;
(2)若c=2,且△ABC为锐角三角形,求a+b取值范围。
已知函数
(1)求函数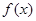 的单调区间和值域。
的单调区间和值域。
(2)设 ,求函数
,求函数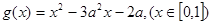 ,若对于任意
,若对于任意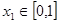 ,总存在
,总存在 ,使得
,使得 成立,求实数
成立,求实数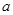 的取值范围。
的取值范围。
已知椭圆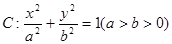 的右焦点为
的右焦点为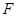 ,离心率
,离心率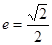 ,椭圆
,椭圆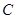 上的点到
上的点到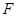 距离的最大值为
距离的最大值为 ,直线
,直线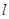 过点
过点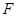 与椭圆
与椭圆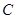 交于不同的两点
交于不同的两点 。
。
(1)求椭圆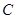 的方程。
的方程。
(2)若 ,求直线
,求直线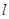 的方程。
的方程。
如图,在四棱锥 中,底面
中,底面 为平行四边形,
为平行四边形,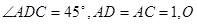 为
为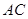 中点,
中点,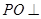 面
面 ,
,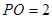 ,
, 为
为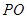 中点。
中点。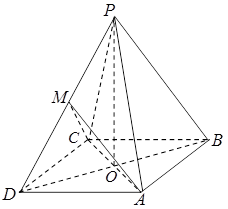
(1)求证: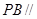 面
面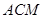 。
。
(2)求证: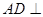 面
面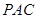 。
。
(3)求直线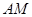 与平面
与平面 所成角的正切值。
所成角的正切值。
 的三个内角
的三个内角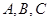 的对边分别为
的对边分别为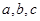 ,
,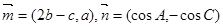 且
且 。
。
(1)求角 的大小。
的大小。
(2)当 取最大值时,求角
取最大值时,求角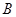 的大小。
的大小。