已知数列{an}的前n项和为Sn, 且满足a1 = 2, nan + 1 = Sn + n(n + 1).
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)设Tn为数列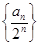 }的前n项和, 求Tn;
}的前n项和, 求Tn;
(Ⅲ)设 , 证明:
, 证明:
选修4-1:几何证明选讲:如图,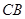 是⊙
是⊙ 的直径,
的直径,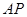 是⊙
是⊙ 的切线,
的切线,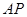 与
与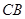 的延长线交于点
的延长线交于点 ,
, 为切点.若
为切点.若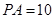 ,
,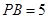 ,
, 的平分线
的平分线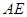 与
与 和⊙
和⊙ 分别交于点
分别交于点 、
、 ,求
,求 的值.
的值.
设函数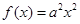 (
(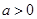 ),
),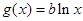 .
.
(1) 将函数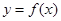 图象向右平移一个单位即可得到函数
图象向右平移一个单位即可得到函数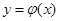 的图象,试写出
的图象,试写出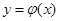 的解析式及值域;
的解析式及值域;
(2) 关于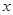 的不等式
的不等式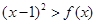 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数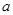 的取值范围;
的取值范围;
(3)对于函数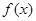 与
与 定义域上的任意实数
定义域上的任意实数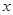 ,若存在常数
,若存在常数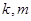 ,使得
,使得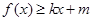 和
和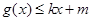 都成立,则称直线
都成立,则称直线 为函数
为函数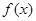 与
与 的“分界线”.设
的“分界线”.设 ,
, ,试探究
,试探究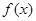 与
与 是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
如图,三棱柱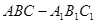 中,
中, ⊥面
⊥面 ,
, ,
, =3,
=3,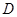 为
为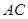 的中点.
的中点. 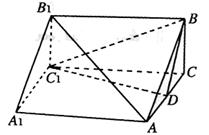
(1)求证: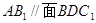 ;
;
(2)求二面角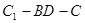 的余弦值;
的余弦值;
(3)在侧棱 上是否存在点
上是否存在点 ,使得
,使得 ?并证明你的结论.
?并证明你的结论.
为了让学生了解更多“奥运会”知识,某中学举行了一次“奥运知识竞赛”,共有800名学生参加了这次竞赛,为了解本次竞赛成绩情况,从中抽取部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表,解答下列问题:
(1)若用系统抽样的方法抽取50个样本,现将所有学生随机地编号为000,001,002,…,799,试写出第二组第一位学生的编号;
(2)填充频率分布表的空格(将答案直接填在表格内),并作出频率分布直方图;
(3)若成绩在85.5~95.5分的学生为二等奖,问参赛学生中获得二等奖的学生约为多少人?
(12分) 如图,在四边形 中,
中,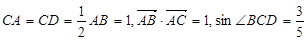 .
.
(1)求边 的长;
的长;
(2)求四边形 的面积;
的面积;
(3)求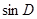 的值.
的值. 