选修4-4: 坐标系与参数方程
在极坐标系中, 已知圆C的圆心C(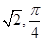 ), 半径r =
), 半径r = .
.
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)若 α ∈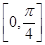 , 直线
, 直线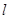 的参数方程为
的参数方程为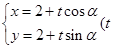 为参数), 直线
为参数), 直线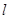 交圆C于A、 B两点, 求弦长|AB|的取值范围.
交圆C于A、 B两点, 求弦长|AB|的取值范围.
已知数列 的各项均为正数,其前
的各项均为正数,其前 ,且
,且 与1的等差中项等于
与1的等差中项等于 与
与
1的等比中项。
(1)求数列 的通项公式;
的通项公式;
(2)设 ,且数列
,且数列 是单调递增数列。试求实数
是单调递增数列。试求实数 的取值范围。
的取值范围。
移动公司进行促销活动,促销方案是:顾客消费1000元,便可获得奖券一张,每张奖券中奖的概率为20%,中奖后移动公司返还顾客现金1000元。小李购买一部价格为2400元的手机,只能获得两张奖券,于是小李补偿50元给同事购买600元的小灵通,可以获得3张奖券,记小李抽奖后的实际开支为 元。
元。
(1)求 的分布列;
的分布列;
(2)试说明小李出资50元便增加一张奖券是否划算?
设 三个内角A,B,C的对边,若向量
三个内角A,B,C的对边,若向量 ,
,
(1)求 的值;
的值;
(2)求 的最大值。
的最大值。
已知函数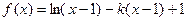 。
。
(1)求函数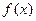 的单调区间;
的单调区间;
(2)若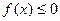 恒成立,试确定实数k的取值范围;
恒成立,试确定实数k的取值范围;
(3)证明:①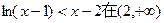 上恒成立
上恒成立
②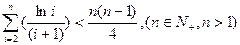
已知椭圆C的中心在原点,焦点在x轴上,它的一个顶点B恰好是抛物线 的焦点,且离心率等于
的焦点,且离心率等于 ,直线
,直线 与椭圆C交于M,N两点。
与椭圆C交于M,N两点。
(1)求椭圆C的方程;
(2)椭圆C的右焦点F是否可以为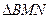 的垂心?若可以,求出直线
的垂心?若可以,求出直线 的方程;若不可以,请说明理由。
的方程;若不可以,请说明理由。