（本题满分14分，第（1）小题5分，第（2）小题9分）
已知圆
，点
，点
在圆
上运动，
的垂直平分线交
于点
．
（1）求动点的轨迹
方程；
（2）过点
且斜率为
的动直线
交曲线于
两点，在
轴上是否存在定点
，使以
为直径的圆恒过这个点？若存在，请求出点的坐标；若不存在，请说明理由．
（本小题满分10分）
设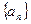
是一个公差为
的等差数列，它的前10项和
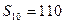
且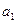
，
，
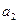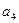成等比数列,求公差
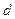的值和数列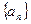的通项公式.
(本小题满分8分)
临汾市染料厂生产化工原料，当年产量在150吨到250吨时，年生产总成本y（万元）与年产量x（吨）之间的关系可近似表示为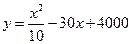
,为使每吨平均成本最低，年产量指标应定在多少吨？（注：平均成本
）
(本小题满分8分)
在△ABC中，若A=120°，AB=5，BC=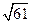
，求△ABC的面积S.
(本小题满分10分)
已知各项均为正数的数列{an}前n项和为Sn，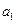
=2，且2，an，Sn成等差数列。
|
（1）求数列{an}的通项公式；
（2）若
，求数列{
}的前n项和Tn；
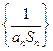的前n项和为
，求证：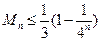
.
（本小题满分10分）
临汾市染料厂生产化工原料，当年产量在150吨到250吨时，年生产总成本
y（万元）与年产量x（吨）之间的关系可近似表示为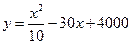
（1）为使每吨平均成本最低，年产量指标应定在多少吨？
（注：平均成本
）
（2）若出厂价为每吨16万元，为获得最大的利润，年产量指标应定在多少吨，
并求出最大利润.