(本题满分18分,第(1)小题4分,第(2)小题5分,第(3)小题9分)
设函数 的定义域为
的定义域为 ,值域为
,值域为 ,如果存在函数
,如果存在函数 ,使得函数
,使得函数 的值域仍是
的值域仍是 ,那么称
,那么称 是函数
是函数 的一个等值域变换.
的一个等值域变换.
(1)判断下列函数 是不是函数
是不是函数 的一个等值域变换?说明你的理由;
的一个等值域变换?说明你的理由; ,
, ;
; ,
, .
.
(2)设函数 的定义域为
的定义域为 ,值域为
,值域为 ,函数
,函数 的定义域为
的定义域为 ,值域为
,值域为 ,那么“
,那么“ ”是否为“
”是否为“ 是
是 的一个等值域变换”的一个必要条件?请说明理由;
的一个等值域变换”的一个必要条件?请说明理由;
(3)设 的定义域为
的定义域为 ,已知
,已知 是
是 的一个等值域变换,且函数
的一个等值域变换,且函数 的定义域为
的定义域为 ,求实数
,求实数 的值.
的值.
已知关于 的方程
的方程 .
.
(1)若方程 表示圆,求实数
表示圆,求实数 的取值范围 ;
的取值范围 ;
(2)若圆 与直线
与直线 相交于
相交于 两点,且
两点,且 ,求
,求 的值
的值
已知x=1是 的一个极值点,
的一个极值点,
(1)求 的值;
的值;
(2)求 的单调递减区间
的单调递减区间
(3)设 试问过点(2,5)可作多少条直线与曲线
试问过点(2,5)可作多少条直线与曲线 相切?请说明理由.
相切?请说明理由.
已知椭圆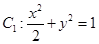 ,抛物线
,抛物线 ,点
,点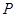 是
是 上的动点,过
上的动点,过
点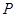 作抛物线
作抛物线 的切线
的切线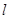 ,交椭圆
,交椭圆 于
于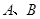 两点,
两点,
(1)当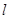 的斜率是
的斜率是 时,求
时,求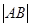 ;
;
(2)设抛物线 的切线方程为
的切线方程为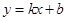 ,当
,当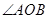 是锐角时,求
是锐角时,求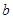 的取值范围.
的取值范围.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,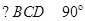 ,
,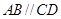 ,
,
又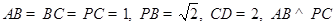 .
.
(Ⅰ)求证: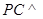 平面
平面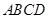 ;
;
(Ⅱ)求点B到平面PAD的距离. 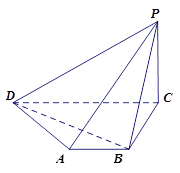
甲、乙两名工人加工同一种零件,两人每天加工的零件数相等,所出次品数分别为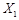 ,
,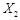 ,且
,且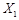 和
和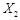 的分布列为:
的分布列为:
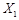 |
0 |
1 |
2 |
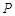 |
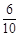 |
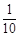 |
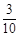 |
试比较两名工人谁的技术水平更高.