如图,椭圆E: 的离心率是 ,点 在短轴 上,且

(Ⅰ)求椭圆
的方程;
(Ⅱ)设
为坐标原点,过点
的动直线与椭圆交于
两点.是否存在常数
,使得
为定值?若存在,求
的值;若不存在,请说明理由.
(本小题满分16分)已知数列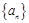 的前
的前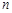 项和
项和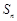 满足:
满足: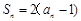 ,数列
,数列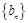 满足:对任意
满足:对任意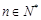 有
有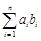
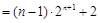 .
.
(1)求数列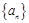 与数列
与数列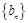 的通项公式;
的通项公式;
(2)记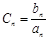 ,数列
,数列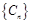 的前
的前 项和为
项和为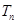 ,证明:当
,证明:当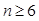 时,
时,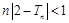 .
.
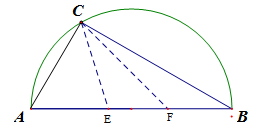
(本小题满分16分)如图,有一直径为8米的半圆形空地,现计划种植甲、乙两种水果,已知单位面积种植甲水果的经济价值是种植乙水果经济价值的5倍,但种植甲水果需要有辅助光照.半圆周上的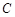 处恰有一可旋转光源满足甲水果生长的需要,该光源照射范围是
处恰有一可旋转光源满足甲水果生长的需要,该光源照射范围是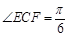 ,点
,点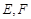 在直径
在直径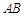 上,且
上,且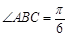 .
.
(1)若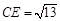 ,求
,求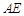 的长;
的长;
(2)设 , 求该空地产生最大经济价值时种植甲种水果的面积.
, 求该空地产生最大经济价值时种植甲种水果的面积.
(本小题满分16分)对于函数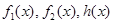 ,如果存在实数
,如果存在实数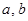 使得
使得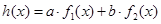 ,那么称
,那么称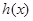 为
为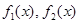 的生成函数.
的生成函数.
(1)下面给出两组函数,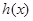 是否分别为
是否分别为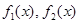 的生成函数?并说明理由;
的生成函数?并说明理由;
第一组: ;
;
第二组: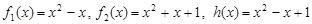 ;
;
(2)设 ,生成函数
,生成函数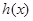 .若不等式
.若不等式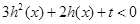 在
在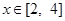 上有解,求实数
上有解,求实数 的取值范围.
的取值范围.
(本小题满分14分)下面的茎叶图记录了甲、乙两代表队各10名同学在一次英语听力比赛中的成绩(单位:分).已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.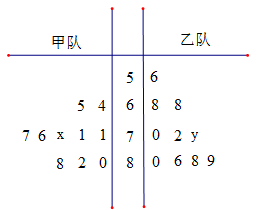
(1)求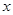 ,
,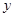 的值;
的值;
(2)若分别从甲、乙两队随机各抽取1名成绩不低于80分的学生,求抽到的学生中,甲队学生成绩不低于乙队学生成绩的概率;
(3)判断甲、乙两队谁的成绩更稳定,并说明理由(方差较小者稳定).
在平面直角坐标系上,第二象限角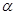 的终边与单位圆交于点
的终边与单位圆交于点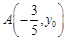 .
.
(1)求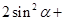
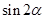 的值;
的值;
(2)若向量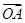 与
与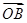 夹角为
夹角为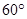 ,且
,且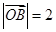 ,求直线
,求直线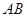 的斜率.
的斜率.