(本小题满分13分)已知函数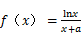 (
(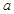 为常数)在点(1,f(1))处的切线的斜率为
为常数)在点(1,f(1))处的切线的斜率为 ,
,
(Ⅰ)求实数a的值;
(Ⅱ)若函数 在区间
在区间 上有极值,求
上有极值,求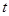 的取值范围.
的取值范围.
(本小题满分13分)某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下: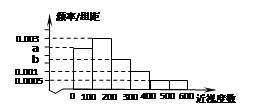
| 近视度数 |
0–100 |
100–200 |
200–300 |
300–400 |
400以上 |
| 学生频数 |
30 |
40 |
20 |
10 |
0 |
将近视程度由低到高分为4个等级:当近视度数在0-100时,称为不近视,记作0;当近视度数在100-200时,称为轻度近视,记作1;当近视度数在200-400时,称为中度近视,记作2;当近视度数在400以上时,称为高度近视,记作3.
(Ⅰ)从该校任选1名高二学生,估计该生近视程度未达到中度及以上的概率;
(Ⅱ)设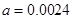 ,从该校任选1名高三学生,估计该生近视程度达到中度或中度以上的概率;
,从该校任选1名高三学生,估计该生近视程度达到中度或中度以上的概率;
(Ⅲ)把频率近似地看成概率,用随机变量 分别表示高二、高三年级学生的近视程度,若
分别表示高二、高三年级学生的近视程度,若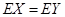 ,求
,求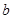 .
.
(本小题满分14分)如图1,在边长为 的正方形
的正方形 中,
中,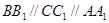 ,且
,且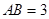 ,且
,且 ,
,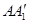 分别交
分别交 于点
于点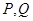 ,将该正方形沿
,将该正方形沿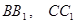 折叠,使得
折叠,使得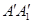 与
与 重合,构成图
重合,构成图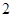 所示的三棱柱
所示的三棱柱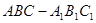 ,在图
,在图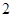 中.
中.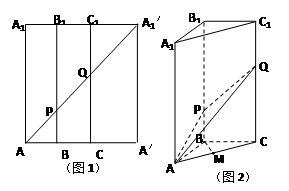
(Ⅰ)求证: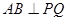 ;
;
(Ⅱ)求直线 与平面
与平面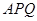 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在底边 上有一点
上有一点 ,使得
,使得 平面
平面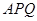 ,求
,求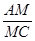 的值.
的值.
(本小题满分13分)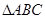 中,
中, ,
, .
.
(Ⅰ)若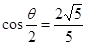 ,
, ,求
,求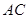 的长度;
的长度;
(Ⅱ)若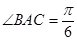 ,
,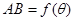 ,求
,求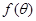 的最大值.
的最大值.
有三个车队分别有2辆、3辆、4辆车,现分别从其中两个车队各抽调两辆车执行
任务,则不同的抽调方案共有种.