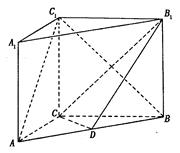
设
,函数
.
(1)求
的单调区间;
(2)证明
在
上仅有一个零点;
(3)若曲线
在点
处的切线与
轴平行,且在点
处的切线与直线
平行,(
是坐标原点),证明:
.
已知函数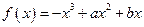 在区间
在区间 内,当
内,当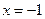 时取得极小值,当
时取得极小值,当 时取得极大值。
时取得极大值。
(1)求函数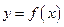 在
在 时的对应点的切线方程。
时的对应点的切线方程。
(2)求函数 在
在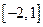 上的最大值与最小值。
上的最大值与最小值。
.(本小 题满分14分)
题满分14分)
已知 且方程
且方程 有两个实根为
有两个实根为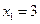 ,
,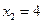 (这里
(这里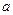 、
、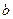 为常数).
为常数).
(1)求函数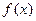 的解析式(2)求函数
的解析式(2)求函数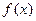 的值域.
的值域.
14分)
(1)已知 是奇函数,求常数m的值;
是奇函数,求常数m的值;
(2)画出函数 的图象,并利用图象回答:
的图象,并利用图象回答:
k为何值时,方程|3x-1|=k无解?有一解?有两解?
(本小题满分12分)
为应对金融危机,刺激消费,某市给市民发放旅游消费卷,由抽样调查预计老、中、青三类市民持有这种消费卷到某旅游景点消费额及其概率如下表:
  |
200元 |
300元 |
400元 |
500元 |
| 老年 |
0.4 |
0.3 |
0.2 |
0.1 |
| 中年 |
0.3 |
0.4 |
0.2 |
0.1 |
| 青年 |
0.3 |
0.3 |
0.2 |
0.2 |
某天恰好有持有这种消费卷的老年人、中年人、青年人各一人到该旅游景点,
(Ⅰ)求这三人消费总额大于1300元的概率;
(Ⅱ)设这三人中消费额大于300元的人数为 ,求
,求 的分布列及数学期望。
的分布列及数学期望。
(本小题满分12分)
如图, 在直三棱柱ABC-A1B1C1中,AC=3 ,BC=4,
,BC=4, ,AA1=4,点D是AB的中点.
,AA1=4,点D是AB的中点.
(Ⅰ)求证:AC⊥BC1;
(Ⅱ)求二面角 的余弦值.
的余弦值.