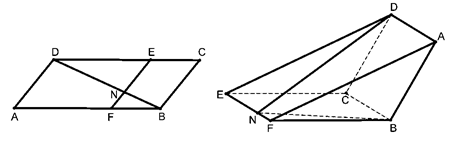
(本小题满分12分)国家AAAAA级八里河风景区五一期间举办“管仲杯”投掷飞镖比赛.每3人组成一队,每人投掷一次.假设飞镖每次都能投中靶面,且靶面上每点被投中的可能性相同.某人投中靶面内阴影区域记为“成功”(靶面正方形 如图所示,其中阴影区域的边界曲线近似为函数
如图所示,其中阴影区域的边界曲线近似为函数 的图像).每队有3人“成功” 获一等奖,2人“成功” 获二等奖,1人“成功” 获三等奖,其他情况为鼓励奖(即四等奖)(其中任何两位队员“成功”与否互不影响).
的图像).每队有3人“成功” 获一等奖,2人“成功” 获二等奖,1人“成功” 获三等奖,其他情况为鼓励奖(即四等奖)(其中任何两位队员“成功”与否互不影响).
( )求某队员投掷一次“成功”的概率;
)求某队员投掷一次“成功”的概率;
( )设
)设 为某队获奖等次,求随机变量
为某队获奖等次,求随机变量 的分布列及其期望.
的分布列及其期望.
如图示,已知平行四边形ABCD和矩形ACEF所在平面互相垂直,AB=1,AD=2,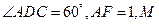 是线段EF的中点.
是线段EF的中点.
(1)求证: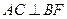 ;(2)设二面角A—FD—B的大小为
;(2)设二面角A—FD—B的大小为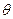 ,求
,求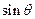 的值;
的值;
(3)设点P为一动点,若点P从M出发,沿棱按照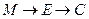 的路线运动到点C,求这一过程中形成的三棱锥P—BFD的体积的最小值.
的路线运动到点C,求这一过程中形成的三棱锥P—BFD的体积的最小值.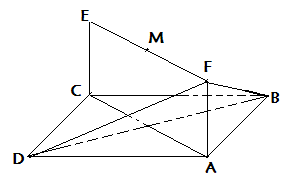
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上40件产品作为样本,称出它们的重量(单位:克),重量的分组区间为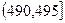 ,
,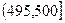 ,…,
,…,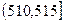 ,由此得到样本的频率分布直方图,如右图所示.
,由此得到样本的频率分布直方图,如右图所示.
(1)根据频率分布直方图,求重量超过505克的产品数量.
(2)在上述抽取的40件产品中任取2件,设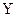 为重量超过505克的产品数量,求
为重量超过505克的产品数量,求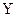 的分布列.
的分布列.
(3)从流水线上任取5件产品,求恰有2件产品的重量超过505克的概率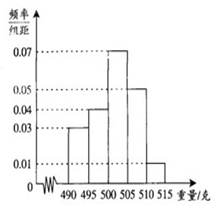
已知向量 ,
,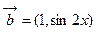 ,函数
,函数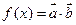 ,
,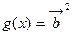 .
.
(Ⅰ)求函数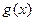 的最小正周期;
的最小正周期;
(Ⅱ)在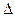
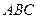 中,
中, 分别是角
分别是角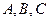 的对边,且
的对边,且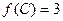 ,
, ,
,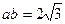 ,且
,且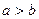 ,求
,求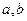 的值.
的值.
(本小题满分14分)已知函数 .
.
(Ⅰ)当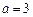 时,求
时,求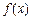 的单调递增区间;
的单调递增区间;
(Ⅱ)求证:曲线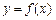 总有斜率为
总有斜率为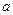 的切线;
的切线;
(Ⅲ)若存在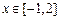 ,使
,使 成立,求
成立,求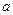 的取值范围.
的取值范围.
如图,已知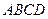 为平行四边形,
为平行四边形,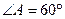 ,
,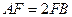 ,
,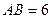 ,点
,点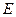 在
在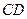 上,
上, ,
, ,
,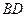 交
交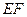 于点
于点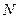 ,现将四边形
,现将四边形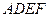 沿
沿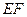 折起,使点
折起,使点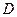 在平面
在平面 上的射影恰在直线
上的射影恰在直线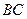 上.
上.
(Ⅰ) 求证: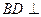 平面
平面 ;
;
(Ⅱ) 求折后直线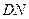 与直线
与直线 所成角的余弦值;
所成角的余弦值;
(Ⅲ) 求三棱锥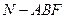 的体积.
的体积.