(本题满分13分)
设椭圆 :
: 
 过
过 ,
, 两点,其中
两点,其中 为椭圆的
为椭圆的
离心率, 为坐标原点.
为坐标原点.
(I)求椭圆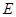 的方程;
的方程;
(II)过椭圆右焦点 的一条直线
的一条直线 与椭圆交于
与椭圆交于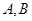 两点,若
两点,若 ,求弦
,求弦 的长.
的长.
已知向量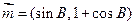 与向量
与向量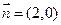 的夹角为
的夹角为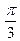 ,
,
在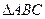 中,
中,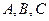 所对的边分别为
所对的边分别为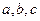 且
且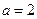 .(改编成)
.(改编成)
(I)求角B的大小;
(Ⅱ)若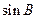 是
是 和
和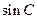 的等比中项,求
的等比中项,求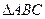 的面积。
的面积。
如图所示,正方形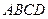 和矩形
和矩形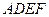 所在平面相互垂直,
所在平面相互垂直,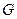 是
是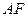 的中点.
的中点.
(I)求证: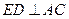 ;
;
(Ⅱ)若直线 与平面
与平面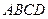 成45o角,求异面直线
成45o角,求异面直线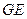 与
与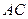 所成角的余弦值.
所成角的余弦值.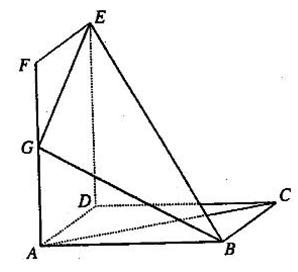
如图,棱柱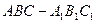 的侧面
的侧面 是菱形,
是菱形,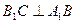 。
。
(1)证明:平面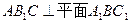 ;
;
(2)设D是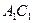 上的点且
上的点且 ,求
,求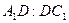 的值。
的值。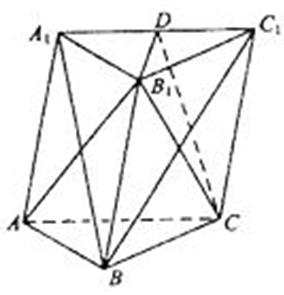
已知△ABC中∠ACB=90°,SA⊥面ABC,AD⊥SC,求证:AD⊥面SBC。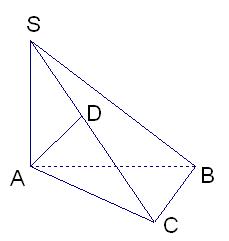
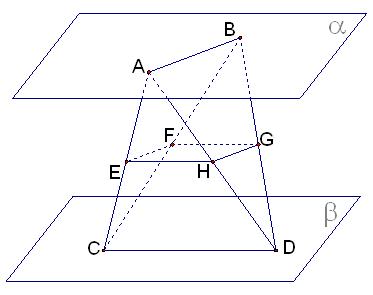
如图:已知平面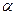 //平面
//平面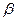 ,点A、B在平面
,点A、B在平面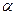 内,点C、D在
内,点C、D在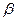 内,直线AB与CD是异面直线,点E、F、G、H分别是线段AC、BC、BD、AD的中点,
内,直线AB与CD是异面直线,点E、F、G、H分别是线段AC、BC、BD、AD的中点,
求证:(Ⅰ)E、F、G、H四点共面;
(Ⅱ)平面EFGH//平面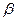 .
.