(本小题满分13分)
已知椭圆 的左、右顶点分别为
的左、右顶点分别为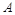 ,
,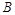 ,右焦点为
,右焦点为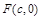 ,点
,点 是椭圆
是椭圆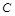 上异于
上异于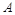 ,
,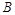 的动点,过点
的动点,过点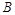 作椭圆
作椭圆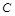 的切线
的切线 ,直线
,直线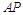 与直线
与直线 的交点为
的交点为 ,且当
,且当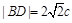 时,
时,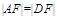 .
.
(Ⅰ)求椭圆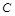 的方程;
的方程;
(Ⅱ)当点 运动时,试判断以
运动时,试判断以 为直径的圆与直线
为直径的圆与直线 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
某市为了了解“陕西分类招生考试”宣传情况,从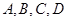 四所中学的学生当中随机抽取50名学生参加问卷调查,已知
四所中学的学生当中随机抽取50名学生参加问卷调查,已知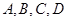 四所中学各抽取的学生人数分别为15,20,10,5.
四所中学各抽取的学生人数分别为15,20,10,5.
(Ⅰ)从参加问卷调查的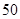 名学生中随机抽取两名学生,求这两名学生来自同一所中学的概率;
名学生中随机抽取两名学生,求这两名学生来自同一所中学的概率;
(Ⅱ)在参加问卷调查的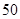 名学生中,从来自
名学生中,从来自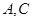 两所中学的学生当中随机抽取两名学生,用
两所中学的学生当中随机抽取两名学生,用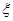 表示抽得
表示抽得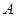 中学的学生人数,求
中学的学生人数,求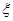 的分布列及期望值.
的分布列及期望值.
已知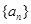 是一个单调递增的等差数列,且满足
是一个单调递增的等差数列,且满足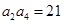 ,
, ,数列
,数列 的前
的前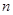 项和为
项和为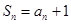
 ,数列
,数列 满足
满足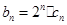 .
.
(Ⅰ)求数列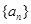 的通项公式;(Ⅱ)求数列
的通项公式;(Ⅱ)求数列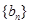 的前
的前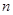 项和.
项和.
选修4—5:不等式选讲
已知函数 ,
,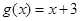 .
.
(Ⅰ)当 时,求不等式
时,求不等式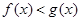 的解集;
的解集;
(Ⅱ)设 ,且当
,且当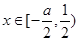 时,
时, ,求a的取值范围.
,求a的取值范围.
选修4—4:坐标系与参数方程
已知曲线C1的参数方程为 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为 .
.
(Ⅰ)把C1的参数方程化为极坐标方程;(Ⅱ)求C1与C2交点的极坐标( ).
).
选修4—1:几何证明选讲
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.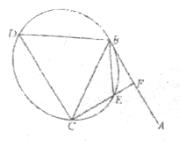
(Ⅰ)证明:DB=DC;
(Ⅱ)设圆的半径为1,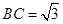 ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.