某商店经营一种成本为每千克40美元的水产品,根据市场分析,若按每千克50元销售,一个月能售出500千克;销售价每涨1元,月销售量就减少10千克,
(1)针对这种水产品的销售情况,设销售单价定为x元(x>50),请用的x代数式表示月销售量,以及获得的利润.
(2)当x取什么数时利润最大?最大利润是多少?
如图,在△ABC中,AB=AC=8,BC=6,点D为BC上一点,BD=2.过点D作射线DE交AC于点E,使∠ADE=∠B.求线段EC的长度.
如图,AB是半圆O的直径,点P(不与点A,B重合)为半圆上一点.将图形沿BP折叠,分别得到点A,O的对称点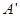 ,
,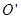 .设∠ABP =α.
.设∠ABP =α.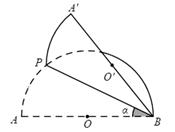
(1)当α=10°时,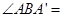 °;
°;
(2)当点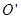 落在
落在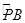 上时,求出
上时,求出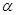 的度数.
的度数.
已知二次函数 .
.
(1)将 化成
化成 的形式;
的形式;
(2)当 时,
时, 的最小值是,最大值是;
的最小值是,最大值是;
(3)当 时,写出
时,写出 的取值范围.
的取值范围.
如图,正方形网格中的每个小正方形的边长都是1,顶点叫做格点.△ABC的三个顶点A,B,C都在格点上.将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.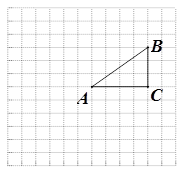
(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过的区域的面积.
如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交 轴
轴
于 两点,点
两点,点 在⊙
在⊙ 上.
上.
(1)求出 两点的坐标;
两点的坐标;
(2)试确定经过A、B且以点P为顶点的抛物线解析式;
(3)在该抛物线上是否存在一点 ,使线段
,使线段 与
与 互相平分?若存在,求出点
互相平分?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.