设二次函数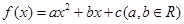 满足条件:①当
满足条件:①当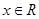 时,
时,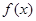 的最大值为0,且
的最大值为0,且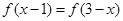 成立;②二次函数
成立;②二次函数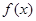 的图象与直线
的图象与直线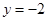 交于
交于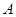 、
、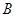 两点,且
两点,且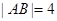 .
.
(Ⅰ)求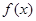 的解析式;
的解析式;
(Ⅱ)求最小的实数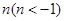 ,使得存在实数
,使得存在实数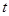 ,只要当
,只要当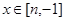 时,就有
时,就有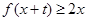 成立.
成立.
已知定点F(3,0)和动点P(x,y),H为PF的中点,O为坐标原点,且满足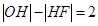 .
.
(1)求点P的轨迹方程;
(2)过点F作直线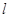 与点P的轨迹交于A,B两点,点C(2,0).连接AC,BC与直线
与点P的轨迹交于A,B两点,点C(2,0).连接AC,BC与直线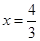 分别交于点M,N.试证明:以MN为直径的圆恒过点F.
分别交于点M,N.试证明:以MN为直径的圆恒过点F.
如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,PA=2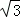 ,BC=CD=2,∠ACB=∠ACD=
,BC=CD=2,∠ACB=∠ACD= .
.
(1)求证:BD⊥平面PAC;
(2)若侧棱PC上的点F满足PF=7FC,求三棱锥P﹣BDF的体积.
对某校高中学生进行心理障碍测试得到如下的列联表:
| 有心理障碍 |
没有心理障碍 |
总计 |
|
| 女生 |
10 |
30 |
|
| 男生 |
70 |
80 |
|
| 总计 |
20 |
110 |
将表格填写完整,试说明心理障碍与性别的关系?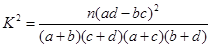
假设检验中的临界值表:
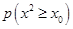 |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706[ |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
已知函数 ,
, ,
,
(1)求实数a的值;
(2)求函数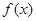 在
在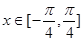 的值域。
的值域。
已知函数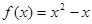 ,
,
(1)求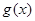 的最大值及相应
的最大值及相应 的值;
的值;
(2)对任意的正数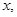 恒有
恒有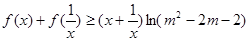 ,求实数
,求实数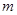 的最大值.
的最大值.