已知:如图9,等腰梯形ABCD的边BC在x轴上,点A在y轴的正方向上,A( 0, 6 ),D ( 4,6),且AB=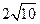
 .
.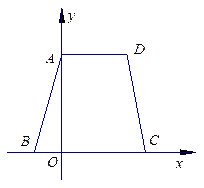
(1)求点B的坐标;
(2)求经过A、B、D三点的抛物线的解析式;
(3)在(2)中所求的抛物线上是否存在一点P,
|
使得 ?若存在,请求出该点坐标,
?若存在,请求出该点坐标,
今年,我国政府为减轻农民负担,决定在5年内免去农业税.某乡今年人均上缴农业税25元,若两年后人均上缴农业税为16元,假设这两年降低的百分率相同.
(1)求降低的百分率;
(2)若小红家有4人,明年小红家减少多少农业税?
(3)小红所在的乡约有16000农民,问该乡农民明年减少多少农业税.
某中学在一次法律知识测试中,抽取部分学生成绩(分数为整
数,满分100分)将所得得数据整理后,画出频率分布直方图,已
知图中从左到右的三个小组的频率分别为0.04,0.06,0.82,第二
小组的频数为3.
(1)本次测试中抽样的学生有多少人?
(2)分数在90.5~100.5这一组的频率是多少?有多少人?
(3)若这次成绩在80分以上(含80分)为优秀,则优秀率不低于多少?
先化简,再求值.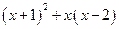 ,其中
,其中 .
.
解不等式组 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.