(本小题满分13分) 某生产流水线由于改进了设备,预计改进后第一年年产量的增长率为 ,以后每年的增长率是前一年的一半,设原来的产量是
,以后每年的增长率是前一年的一半,设原来的产量是
(Ⅰ) 写出改进设备后的第一年、第二年、第三年的产量,并写出第 年与第
年与第 年的产量之间的关系式
年的产量之间的关系式 ;
;
(Ⅱ) 由于设备不断老化,估计每年将损失年产量的 ,如此下去,以后每年的产量是否始终是逐年提高?若是,请给予证明;若不是,请说明从第几年起,产量将比上一年减少?
,如此下去,以后每年的产量是否始终是逐年提高?若是,请给予证明;若不是,请说明从第几年起,产量将比上一年减少?
设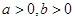 ,且
,且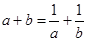 .
.
(1)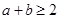 ;
;
(2)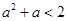 与
与 不可能同时成立.
不可能同时成立.
已知直线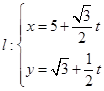 (
(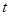 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,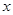 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线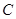 的极坐标方程为
的极坐标方程为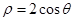 .
.
(1)将曲线C的极坐标方程化为直角坐标方程;
(2)设点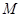 的直角坐标为
的直角坐标为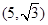 ,直线
,直线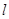 与曲线C 的交点为
与曲线C 的交点为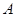 ,
,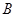 ,求
,求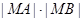 的值.
的值.
如图,在圆 中,相交于点
中,相交于点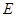 的两弦
的两弦 ,
,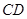 的中点分别是
的中点分别是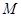 ,
, ,直线
,直线 与直线
与直线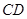 相交于点
相交于点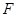 ,证明:
,证明: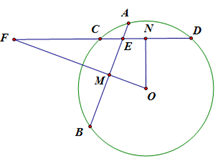
(1) ;
;
(2)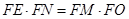 .
.
若定义在 上的函数
上的函数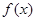 满足
满足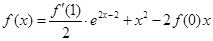 ,
,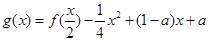 ,
,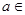
 .
.
(Ⅰ)求函数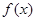 解析式;
解析式;
(Ⅱ)求函数 单调区间;
单调区间;
(Ⅲ)若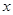 、
、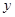 、
、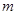 满足
满足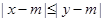 ,则称
,则称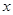 比
比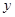 更接近
更接近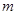 .当
.当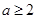 且
且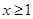 时,试比较
时,试比较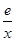 和
和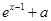 哪个更接近
哪个更接近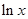 ,并说明理由.
,并说明理由.
已知椭圆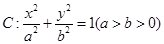 的下顶点为
的下顶点为 ,
,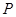 到焦点的距离为
到焦点的距离为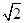 .
.
(Ⅰ)设Q是椭圆上的动点,求 的最大值;
的最大值;
(Ⅱ)若直线 与圆O:
与圆O: 相切,并与椭圆
相切,并与椭圆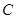 交于不同的两点A、B.当
交于不同的两点A、B.当 ,且满足
,且满足 时,求
时,求 AOB面积S的取值范围.
AOB面积S的取值范围.