(本小题满分13分)已知椭圆 :
: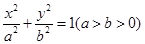 的离心率为
的离心率为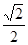 ,过右焦点
,过右焦点 的直线
的直线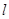 与
与 相交于
相交于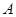 ,
, 两点,当
两点,当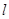 的斜率为
的斜率为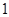 时,坐标原点
时,坐标原点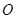 到
到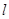 的距离为
的距离为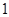 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2) 上是否存在点
上是否存在点 ,使得当
,使得当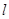 绕
绕 转到某一位置时,有
转到某一位置时,有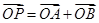 成立?若存在,求出所有的
成立?若存在,求出所有的 的坐标与
的坐标与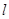 的方程;若不存在,说明理由,
的方程;若不存在,说明理由,
在锐角 中,角
中,角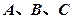 的对边分别为
的对边分别为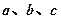 ,且
,且 成等差数列。(1)求角
成等差数列。(1)求角 的大小;(2)求
的大小;(2)求 的取值范围
的取值范围
某水库进入汛期的水位升高量hn (标高)与进入汛期的天数n的关系是hn=20 ,汛期共计约40天,当前水库水位为220(标高),而水库警戒水位是400(标高),水库共有水闸15个,每开启一个泄洪,一天可使水位下降4(标高).
,汛期共计约40天,当前水库水位为220(标高),而水库警戒水位是400(标高),水库共有水闸15个,每开启一个泄洪,一天可使水位下降4(标高).
(I)若不开启水闸泄洪,这个汛期水库是否有危险?若有危险,将发生在第几天?
(II)若要保证水库安全,则在进入汛期的第一天起每天至少应开启多少个水闸泄洪?
(参考数据:2.272=5.1529,2.312=5.3361)
已知在数列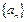 中,
中,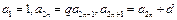 (
(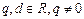 ).
).
(I)若q =2,d = -1,,求a3,a4,并猜测a2006;
(II)若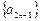 是等比数列,且
是等比数列,且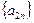 是等差数列,求q, d满足的条件.
是等差数列,求q, d满足的条件.
政府决定用“对社会贡献率”对企业进行
评价,用an表示某企业第n年投入的治理污染费用,用bn表示该企业第n
年的产值。设a1 = a(万元),且以后治理污染费用每年都比上一年增加3a
(万元);又设b1 = b(万元),且企业的产值每年均比上一年增长10%,用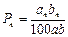 表示企业第n年“对社会贡献率”.
表示企业第n年“对社会贡献率”.
(I)求该企业第一年和第二年的“对社会贡献率”;
(II)试问:从第几年起该企业“对社会贡献率”不低于30%?
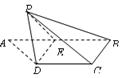
如图,梯形ABCD中,CD//AB,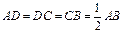 ,E是AB的中点,将△ADE沿DE折起,使点A折到点P的位置,且二面角
,E是AB的中点,将△ADE沿DE折起,使点A折到点P的位置,且二面角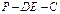 的大小为1200.
的大小为1200.
(I)求证: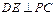 ;
;
(II)求直线PD与平面BCDE所成角的大小;
(III)求点D到平面PBC的距离.