已知
，不等式
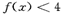的解集为M .
(I)求M;
(II)当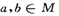
时，证明：
.
当实数
取何值时，复数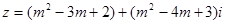
（其中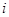
是虚数单位）．
（1）是实数；（2）是纯虚数；（3）等于零.
已知圆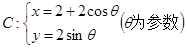
，直线l: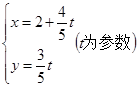
（1）求圆C的普通方程.若以原点为极点，以x轴的正半轴为极轴建立极坐标系，写出圆C的极坐标方程.
（2）判断直线l与圆C的位置关系，并说明理由；若相交，请求出弦长
如图，BA是⊙O的直径，AD是切线，BF、BD是割线，求证：BE•BF=BC•BD．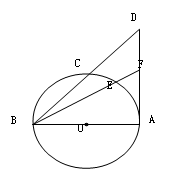
（Ⅰ）已知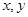
都是正实数，求证：
；
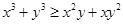（2）已知a,b,c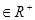
,且a+b+c="1," 求证：a2+b2+c2≥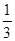
已知函数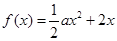
， 
．
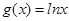（Ⅰ）如果函数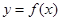
在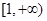
上是单调函数，求
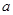的取值范围；
（Ⅱ）是否存在正实数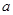，使得函数
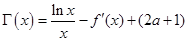在区间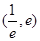
内有两个不同的零点？若存在，请求出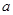的取值范围；若不存在，请说明理由