( 本小题满分12分))设不等式 确定的平面区域为
确定的平面区域为 ,
,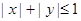 确定的平面区域为
确定的平面区域为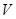 .
.
(Ⅰ)定义坐标为整数的点为整点
(1)在区域 内任取1个整点
内任取1个整点 ,求满足
,求满足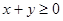 的概率
的概率
(2)在区域 内任取2个整点,求这两个整点中恰有1个整点在区域
内任取2个整点,求这两个整点中恰有1个整点在区域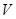 内的概率
内的概率
(Ⅱ) 在区域 内任取一个点,求此点在区域
内任取一个点,求此点在区域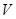 的概率.
的概率.
从分别写上数字1,2,3,…,9的9张卡片中,任取2张,观察上面数字,试求下列事件的概率:
(1)两数和为偶数;
(2)两数积为完全平方数。
下表是某种油菜子在相同条件下的发芽试验结果表,请完成表格并回答题。
| 每批粒数 |
2 |
5 |
10 |
70 |
130 |
700 |
1500 |
2000 |
3000 |
| 发芽的粒数 |
2 |
4 |
9 |
60 |
116 |
282 |
639 |
1339 |
2715 |
| 发芽的频率 |
(1)完成上面表格:
(2)该油菜子发芽的概率约是多少?
等边三角形 的边长为
的边长为 ,沿平行于
,沿平行于 的线段
的线段 折起,使平面
折起,使平面 平面
平面 ,设点
,设点 到直线
到直线 的距离为
的距离为 ,
, 的长为
的长为 .
.
(1) 为何值时,
为何值时, 取得最小值,最小值是多少;
取得最小值,最小值是多少;
(2)若 ,求
,求 的最小值.
的最小值.
表面积为 的多面体的每一个面都外切于半径为
的多面体的每一个面都外切于半径为 的一个球,求这个多面体的体积.
的一个球,求这个多面体的体积.
如图,直三棱柱 中,
中, ,
, ,
, ,侧棱
,侧棱 ,侧面
,侧面 的两条对角线交点为
的两条对角线交点为 ,
, 的中点为
的中点为 .
.
求证: 平面
平面 .
.
 |