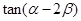(本小题满分12分)某同学参加语、数、外三门课程的考试,设该同学语、数、外取得优秀成绩的概率分别为 ,m,n(m>n),设该同学三门课程都取得优秀成绩的概率为
,m,n(m>n),设该同学三门课程都取得优秀成绩的概率为 ,都未取得优秀成绩的概率为
,都未取得优秀成绩的概率为 ,且不同课程是否取得优秀成绩相互独立.
,且不同课程是否取得优秀成绩相互独立.
(1)求m,n;
(2)设X为该同学取得优秀成绩的课程门数,求EX.
(本小题满分14分) 某民营企业生产甲、乙两种产品,根据市场调查与预测,甲产品的利润与投资成正比,其关系如图①;乙产品的利润与投资的算术平方根成正比,其关系如图②.
某民营企业生产甲、乙两种产品,根据市场调查与预测,甲产品的利润与投资成正比,其关系如图①;乙产品的利润与投资的算术平方根成正比,其关系如图②.
(1)分别将 、
、 两产品的利润表示为投资量的函数关系式;
两产品的利润表示为投资量的函数关系式;
(2)该公司已有10万元资金,并全部投入 、
、 两种产品中,问:怎样分配这10万元投资,才能使公司获得最大利润?其最大利润为多少万元?
两种产品中,问:怎样分配这10万元投资,才能使公司获得最大利润?其最大利润为多少万元?
(本小题满分14分)已知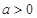 ,函数
,函数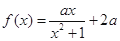 ,
, .
.
(Ⅰ)求函数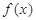 的单调区间;
的单调区间;
(Ⅱ)求证:对于任意的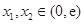 ,都有
,都有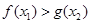 .
.
(本小题满分13分)已知函数 在
在 处取得极值。
处取得极值。
(1)讨论 和
和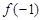 是函数
是函数 的极大值还是极小值;
的极大值还是极小值;
(2)过点 作曲线
作曲线 的切线,求此切线方程。
的切线,求此切线方程。
(本小题满分13分)已知函数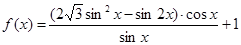 .
.
(1)求 的定义域及最小正周期;
的定义域及最小正周期;
(2)求 在区间
在区间 上的最值.
上的最值.
(本小题满分12分)已知 ,
, 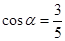 .
. 求下列式子的值
求下列式子的值
(1) ;(2)
;(2)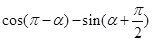 (3)
(3)