如图,直线AB、CD相交于点O,OE平分∠AOD,若∠BOD=100°,求∠AOE的度数.
小明开了一家皮装专卖店,2005年各月份的销售情况如下表:
用合适的统计图表示2005年各季度的销售量变化情况。
宁波港年货物吞吐量位居大陆第二,世界第五;如图是宁波港1994年~2004年货物吞吐量统计图。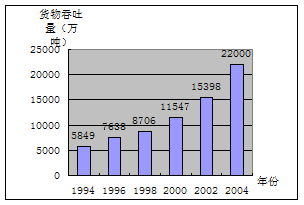
(1)从统计图中你能发现哪些信息,请说出两个。
(2)有人断定宁波港货物吞吐量每两年得平均增长率都不超过15%,你认为他得说法正确吗?请说明理由。
在2008年7月~10月间,沈阳市武汉武汉和武汉市的月平均气温如下表: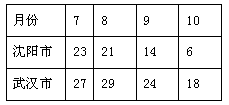
(1)分别画出两市气温变化的折线图和条形图
(2)两市的气温变化有什么特点?
图是2001年南宁市社会消费品零售总额(亿元)统计图
请你仔细观察图中的数据,并回答下列问题:
(1)求1990年、1995年、2000年这三年社会消费品零售总额的平均数(精确到0.01)
(2)从图中你还能发现哪些信息?说出两条。
用折线图描述了某地某日的气温变化情况
(1)这一天的最高气温是多少?什么时候达到最低气温?
(2)估计这一天19时的气温。