如图甲,直线 与 轴、 轴分别交于点 、点 ,经过 、 两点的抛物线 与 轴的另一个交点为 ,顶点为 .
(1)求该抛物线的解析式;
(2)在该抛物线的对称轴上是否存在点 ,使以 , , 为顶点的三角形为等腰三角形?若存在,请直接写出所符合条件的点 的坐标;若不存在,请说明理由;
(3)当 时,在抛物线上求一点 ,使 的面积有最大值(图乙、丙供画图探究).

在平面直角坐标系中,已知抛物线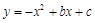 与
与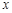 轴交于点
轴交于点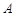 (-1,0)、
(-1,0)、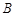 (3,0),与
(3,0),与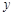 轴的正半轴交于点
轴的正半轴交于点 ,顶点为
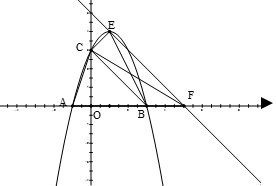
,顶点为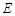 .
.
求抛物线解析式及顶点
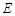 的坐标;
的坐标;如图,过点E作BC平行线,交
 轴于点F,在不添加线和字母情况下,图中面积相等的三角形有:.
轴于点F,在不添加线和字母情况下,图中面积相等的三角形有:.将抛物线向下平移,与
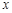 轴交于点M、N,与
轴交于点M、N,与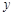 轴的正半轴交于点P,顶点为Q.在四边形MNQP中满足S△NPQ = S△MNP,求此时直线PN的解析式
轴的正半轴交于点P,顶点为Q.在四边形MNQP中满足S△NPQ = S△MNP,求此时直线PN的解析式
如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.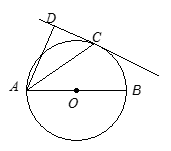
求证:AD⊥DC
若
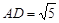 ,
,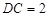 ,求
,求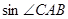 的值以及AB的长.
的值以及AB的长.
某块试验田里的农作物每天的需水量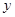 (千克)与生长时间
(千克)与生长时间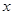 (天)之间的关系如折线图所示.这些农作物在第10天、第30天的需水量分别为2000千克、3000千克,在第40天后每天的需水量比前一天增加100千克.
(天)之间的关系如折线图所示.这些农作物在第10天、第30天的需水量分别为2000千克、3000千克,在第40天后每天的需水量比前一天增加100千克.分别求出
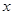 ≤40和
≤40和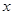 ≥40时
≥40时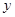 与
与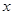 之间的关系式
之间的关系式如果这些农作物每天的需水量大于或等于4000千克时需要进行人工灌溉,那么应从第几天开始进行人工灌溉?
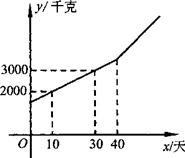
我市教育部门为了了解初三学生身体素质状况,抽取了某校学生进行体育测试。下列图表是该校初三学生的男生1000米跑、女生800米跑的考试成绩中分别抽取的10个数据.
| 考生 编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 男生 成绩 |
3′05〞 |
3′11〞 |
3′53〞 |
3′10〞 |
3′55〞 |
3′30〞 |
3′25〞 |
3′19〞 |
3′27〞 |
3′55〞 |
这10名男生成绩极差为
按《镇江市中学生体育成绩考查》规定,女生800米跑成绩不超过3′35 〞就可以得满分.该校学生有490人,男生比女生少70人. 请你根据上面抽样的结果,估算该校考生中有多少名女生该项考试得满分?
北京时间2011年3月11日13:46,在日本本州岛附近海域发生9.0级强震,中国政府迅速派出救援队前往救援。中国救援队发现在如图所示的展览厅内有一伤者等待救援.救援人员任选一个入口进入展览大厅,救助伤者后任选一个出口离开.
救援人员从进入到离开共有多少种可能的结果?(要求画出表格或树状图)
救援人员从入口A进入展厅并从北出口或西出口离开的概率是多少?