如图，在Rt△ABC中，∠B＝90°，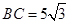
，∠C＝30°．点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒(t＞0)．过点D作DF⊥BC于点F，连接DE、EF．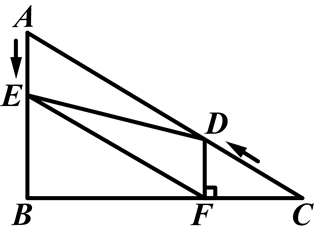
(1)求证：AE＝DF；
(2)四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，请说明理由；
(3)当t为何值时，△DEF为直角三角形？请说明理由．
如图，平行四边形ABCD中，点E是AD的中点，连接BE并延长交CD的延长线于点F．
（1）求证：△ABE≌△
DFE；
（2）连接CE，当CE平分∠BCD时，求证：ED=FD．
某区老年人、成年人、青少年各年龄段的实际人口比是3：5：2，为了解该地区20万读者对工具书、小说、诗歌、漫画四类图书的喜爱情况，按上述比例随即抽取一定数量的读者进行调查（每人只选一类图书
），根据调查结果绘制了两幅尚不完整的统计图：
根据统计图
所提供的信息，完成下列问题；
(1)本次共调查了▲名读者；
（2）补全条形统计图，并计算喜欢小说人数所占的百分比。
（3）估计该地区青少年中喜爱漫画的读者大约有多少名？
在课外活动期间，小英、小丽和小敏在操场上画出A、B两个区域，一
起玩投沙包游戏．沙包落在A区域所得分值与落在B区域所得分值不同．当每人各投沙包
四次时，其落点和四次总分如图所示．请求出小敏的四次总分．
先化简，再求值：
，其中
．
解不等式组，
并写出不等式组的整数解。