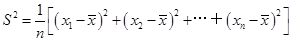如图中图(1),在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.
(1)求证:AF=BE.
(2)如图中图(2),在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.
某销售公司员工的工资如下表:
| 员工人数 |
1 |
1 |
20 |
8 |
| 月工资 |
5000 |
4200 |
1500 |
800 |
(1)分别计算该公司员工月工资的平均数、中位数和众数;
(2)你认为用上题中计算出的哪个数据来代表该公司员工的月工资水平更为合适?请简要说明理由.
26.甲乙两人在相同条件下各射靶10次,甲10次射靶的成绩的情况如图所示,乙10次射靶的成绩依次是:3环、4环、5环、8环、7环、7环、8环、9环、9环、10环.
(1)请在图中画出乙的射靶成绩的折线图.
(2)请将下表填完整:
| 平均数 |
方差 |
中位数 |
命中9环及以上次数 |
|
| 甲 |
7 |
1.2 |
||
| 乙 |
4.8 |
3 |
(3)请从下列三个不同角度对这次测试结果进行分析.
①从平均数和方差相结合看(分析谁的成绩稳定些);
②从平均数和中位数相结合看(分析谁的成绩好些).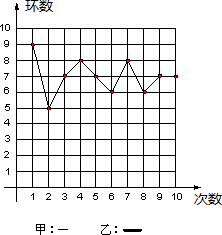
甲、乙两班参加学校迎“青奥”知识比赛,两班的参赛人数相等.比赛结束后,依据两班学生成绩绘制了如下的统计图表.
| 分数 |
6分 |
7分 |
8分 |
9分 |
| 人数 |
1 |
10 |
3 |
6 |
乙班学生迎“青奥”知识比赛成绩统计表
(1)经计算乙班学生的平均成绩为7.7分,中位数为7分,请计算甲班学生的平均成绩、中位数,并从平均数和中位数的角度分析哪个班的成绩较好;
(2)如果学校决定要组织6个人的代表队参加市级团体赛,为了便于管理,决定依据本次比赛成绩仅从这两个班的其中一个班中挑选参赛选手,你认为应选哪个班?请说明理由.
为考察甲、乙两种农作物的长势,分别从中抽取了10株苗,测得苗高如下(单位:cm):
甲:9,10,11,12,7,13,10,8,12,8;
乙:8,13,12,11,10,12,7,7,9,11.
如果你也参加了这次考察,请你经过计算后回答如下问题:
(1)哪种农作物的10株苗长的比较高?
(2)哪种农作的10株苗长的比较整齐?
已知一组数据:6,3,4,7,6,3,5,6
(1)求这组数据的平均数、众数、中位数;
(2)求这组数据的方差和标准差.(方差公式: