甲、乙两家体育器材商店出售同样的乒乓球拍和乒乓球,球拍每副定价50元,乒乓球每盒定价10元,“十一”长假期间,两家商店都搞促销活动:甲商店规定每买一副乒乓球拍赠2盒乒乓球;乙商店规定所有商品9折优惠.某校乒乓球队需要买2副乒乓球拍,乒乓球若干盒(不少于4盒).设该校要买乒乓球x盒,所需商品在甲商店购买需要y1元,在乙商店购买需要y2元.请分别写出y1,y2关于x的函数解析式,并对x的取值情况进行分析,说明在哪一家商店购买所需商品比较便宜.
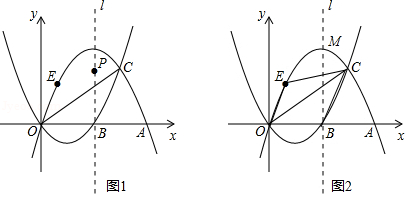
如图1,抛物线 与 相交于点 、 , 与 分别交 轴于点 、 ,且 为线段 的中点.
(1)求 的值;
(2)若 ,求 的面积;
(3)抛物线 的对称轴为 ,顶点为 ,在(2)的条件下:
①点 为抛物线 对称轴 上一动点,当 的周长最小时,求点 的坐标;
②如图2,点 在抛物线 上点 与点 之间运动,四边形 的面积是否存在最大值?若存在,求出面积的最大值和点 的坐标;若不存在,请说明理由.
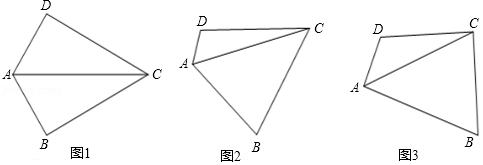
在四边形 中, ,对角线 平分 .
(1)如图1,若 ,且 ,试探究边 、 与对角线 的数量关系并说明理由.
(2)如图2,若将(1)中的条件“ ”去掉,(1)中的结论是否成立?请说明理由.
(3)如图3,若 ,探究边 、 与对角线 的数量关系并说明理由.
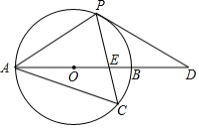
如图,以 边为直径的 经过点 , 是 上一点,连接 交 于点 ,且 , .
(1)试判断 与 的位置关系,并说明理由;
(2)若点 是弧 的中点,已知 ,求 的值.
某公司从2013年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
|
年 度 |
2013 |
2014 |
2015 |
2016 |
|
投入技改资金 (万元) |
2.5 |
3 |
4 |
4.5 |
|
产品成本 (万元 件) |
7.2 |
6 |
4.5 |
4 |
(1)请你认真分析表中数据,从一次函数和反比例函数中确定哪一个函数能表示其变化规律,给出理由,并求出其解析式;
(2)按照这种变化规律,若2017年已投入资金5万元.
①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).
如图,在水平地面上有一幢房屋 与一棵树 ,在地面观测点 处测得屋顶 与树梢 的仰角分别是 与 , ,在屋顶 处测得 .若房屋的高 米,求树高 的长度.
