已知：如图，四边形ABCD是边长为2的菱形，∠BAD＝60°-优题课

已知：如图，四边形ABCD是边长为2的菱形，∠BAD＝60°，对角线AC与BD交于点O，过点O的直线EF交AD于点E，交BC于点F．

（1）求证：△AOE≌△COF；
（2）若∠EOD＝30°，求CE的长．

科目数学题型解答题难度中等

定义：有一组邻边相等，并且它们的夹角是直角的凸四边形叫做等腰直角四边形．

（1）如图1，等腰直角四边形 $ABCD$ ， $AB = BC$ ， $∠ ABC = 90 °$ ，

①若 $AB = CD = 1$ ， $AB / / CD$ ，求对角线 $BD$ 的长．

②若 $AC ⊥ BD$ ，求证： $AD = CD$ ，

（2）如图2，在矩形 $ABCD$ 中， $AB = 5$ ， $BC = 9$ ，点 $P$ 是对角线 $BD$ 上一点，且 $BP = 2 PD$ ，过点 $P$ 作直线分别交边 $AD$ ， $BC$ 于点 $E$ ， $F$ ，使四边形 $ABFE$ 是等腰直角四边形，求 $AE$ 的长．

某农场拟建一间矩形种牛饲养室，饲养室的一面靠现有墙（墙足够长），已知计划中的建筑材料可建围墙的总长为 $50 m$ ．设饲养室长为 $x (m)$ ，占地面积为 $y (m^{2})$ ．

（1）如图1，问饲养室长 $x$ 为多少时，占地面积 $y$ 最大？

（2）如图2，现要求在图中所示位置留 $2 m$ 宽的门，且仍使饲养室的占地面积最大，小敏说：“只要饲养室长比（1）中的长多 $2 m$ 就行了．”请你通过计算，判断小敏的说法是否正确．

如图，学校的实验楼对面是一幢教学楼，小敏在实验楼的窗口 $C$ 测得教学楼顶部 $D$ 的仰角为 $18 °$ ，教学楼底部 $B$ 的俯角为 $20 °$ ，量得实验楼与教学楼之间的距离 $AB = 30 m$ ．

（1）求 $∠ BCD$ 的度数．

（2）求教学楼的高 $BD$ ．（结果精确到 $0.1 m$ ，参考数据： $\tan 20 ° \approx 0.36$ ， $\tan 18 ° \approx 0.32)$

为了解本校七年级同学在双休日参加体育锻炼的时间，课题小组进行了问卷调查（问卷调查表如图所示），并用调查结果绘制了图1，图2两幅统计图（均不完整），请根据统计图解答以下问题：

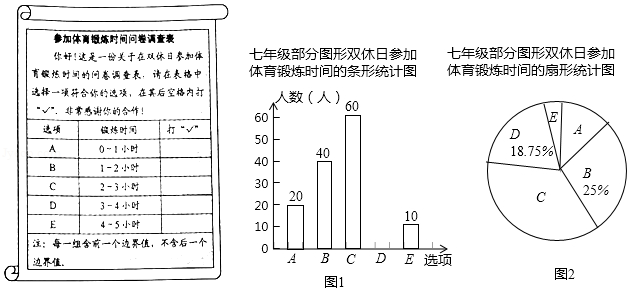
（1）本次接受问卷调查的同学有多少人？补全条形统计图．

（2）本校有七年级同学800人，估计双休日参加体育锻炼时间在3小时以内（不含3小时）的人数．

某市规定了每月用水18立方米以内（含18立方米）和用水18立方米以上两种不同的收费标准．该市的用户每月应交水费 $y$ （元 $)$ 是用水量 $x$ （立方米）的函数，其图象如图所示．

（1）若某月用水量为18立方米，则应交水费多少元？

（2）求当 $x > 18$ 时， $y$ 关于 $x$ 的函数表达式，若小敏家某月交水费81元，则这个月用水量为多少立方米？