随着车辆的增加，交通违规的现象越来越严重，交警对某雷达测速区检测到的一组汽车的时速（千米/时）数据进行整理，得到其频数及频率如表（未完成）：
| 数据段 |
频数 |
频率 |
| 30﹣40 |
10 |
0．05 |
| 40﹣50 |
36 |
|
| 50﹣60 |
|
0．39 |
| 60﹣70 |
|
|
| 70﹣80 |
20 |
0．10 |
| 总计 |
200 |
1 |
（1）请你把表中的数据填写完整；
（2）补全频数分布直方图；
（3）如果汽车时速不低于60千米即为违章，则违章车辆共有多少辆？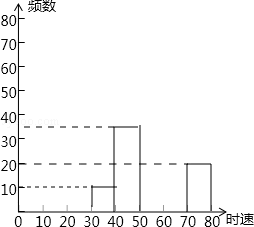
如图，已知抛物线经过A（﹣2，0），B（﹣3，3）及原点O，顶点为C．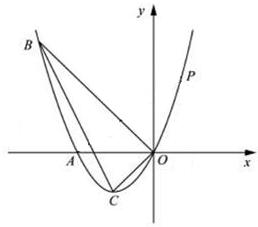
（1）求抛物线的解析式；
（2）若点D在抛物线上，点E在抛物线的对称轴上，且A、O、D、E为顶点的四边形是平行四边形，求点D的坐标；
（3）P是抛物线上的第一象限内的动点，过点P作PMx轴，垂足为M，是否存在点P，使得以P、M、A为顶点的三角形△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．
如图，矩形ABCD的边AB="6" cm，BC="8" cm，在BC上取一点P，在CD边上取一点Q，使∠APQ成直角，设BP="x" cm，CQ="y" cm，试以x为自变量，写出y与x的函数关系式.并求
为何值时，
有最大值或最小值？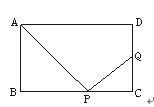
某商场以每件20元的价格购进一种商品，试销中发现，这种商品每天的销售量
(件)与每件的销售价
(元)满足关系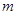：=140－2
．(1)写出商场卖这种商品每天的销售利润
与每件的销售价间的函数关系式；(2)如果商场要想每天获得最大的销售利润，每件商品的售价定为多少最合适？最大销售利润为多少？
如图，△ABC是一张锐角三角形的硬纸片，AD是边BC上的高，BC=40cm,AD=30c
从这张硬纸片上剪下一个长HG是宽HE的2倍的矩形EFGH，使它的一边EF在BC上，
顶点G、H分别在AC，AB上，AD与HG的交点为M．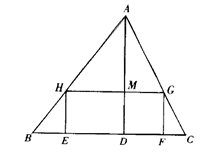
（1）求证：
=
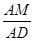（2）求这个矩形EFGH的周长．
已知抛物线
与
轴有两个不同的交点．(1)求
的取值范围；(2)抛物线
与x轴两交点的距离为2，求的值．