已知椭圆 ,离心率
,离心率 ,且过点
,且过点 ,
,
(1)求椭圆方程;
(2) 以
以 为直角顶点,边
为直角顶点,边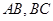 与椭圆交于
与椭圆交于 两点,求
两点,求 面积的最大值.
面积的最大值.
已知函数f(x)=x3+bx2+ax+d的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为6x-y+7=0.(Ⅰ)求函数y=f(x)的解析式;(Ⅱ)求函数y=f(x)的单调区间.
已知定义在R上的函数f(x)=x2(ax-3),其中a为常数.(Ⅰ)若x=1是函数f(x)的一个极值点,求a的值;(Ⅱ)若函数f(x)在区间(-1,0)上是增函数,求a的取值范围.
设函数f(x)=2x3-3(a-1)x2+1,其中a≥1.(Ⅰ)求f(x)的单调区间;(Ⅱ)讨论f(x)的极值.
已知 是一个等差数列,且 .
(Ⅰ)求 的通项
(Ⅱ)求 前 项和 的最大值.
已知A、B、C为三个锐角,且A+B+C=π.若向量=(2-2sinA,cosA+sinA)与向量=(cosA-sinA,1+sinA)是共线向量.(Ⅰ)求角A;(Ⅱ)求函数y=2sin2B+cos的最大值.