函数 ,
,
(1)若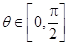 时,求
时,求 的最大值;
的最大值;
(2)设 时,若对任意
时,若对任意 ,都有
,都有 恒成立,且
恒成立,且 的最大值为2,求
的最大值为2,求 的表达式.
的表达式.
已知椭圆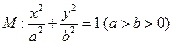 的左右焦点分别
的左右焦点分别 为
为 ,
, .在椭圆
.在椭圆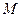 中有一内接三角形
中有一内接三角形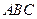 ,其顶点
,其顶点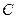 的坐
的坐 标
标 ,
, 所在直线的斜率为
所在直线的斜率为 .
.
(Ⅰ)求椭圆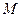 的方程;
的方程;
(Ⅱ)当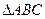 的面积最大时,求直线
的面积最大时,求直线 的方程.
的方程.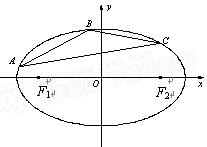
已知函数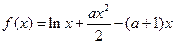 ,
,
 ,且
,且 .
.
(Ⅰ)若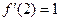 ,求
,求 的值;
的值;
(Ⅱ)当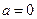 时,求函数
时,求函数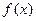 的最大值;
的最大值;
(Ⅲ)求函数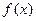 的单调递增区间.
的单调递增区间.
如图,在四棱锥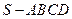 中,底面
中,底面 是正方形,其他四个侧面都是等边三角形,
是正方形,其他四个侧面都是等边三角形,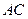 与
与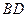 的交点为O.
的交点为O.
(Ⅰ)求证: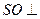 平面
平面 ;
;
(Ⅱ)已知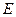 为侧棱
为侧棱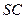 上一个动点. 试问对于
上一个动点. 试问对于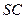 上任意一点
上任意一点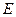 ,平面
,平面 与平面
与平面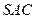 是否垂直?若垂直,请加以证明;若不垂直,请
是否垂直?若垂直,请加以证明;若不垂直,请 说明理由.
说明理由.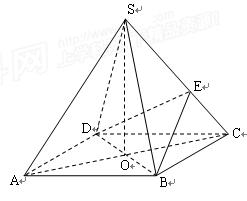
(本题满分1 3分)
3分)
某运动员进行20次射击练习,记录了他射击的有关数据,得到下表:
| 环数 |
7 |
8 |
9 |
10 |
| 命中次数 |
2 |
7 |
8 |
3 |
(Ⅰ)求此运动员射击的环数的平均数;
(Ⅱ)若将表中某一环数所对应的命中次数作为一个结果,在四个结果(2次、7次、8次、3次)中,随机取2个不同的结果作为基本事件进行研究,记这两个结果分别为 次、
次、 次,每个基本事件为(m,n).
次,每个基本事件为(m,n).
求“ ”的概率.
”的概率.
设函数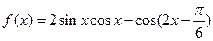 .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)当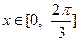 时,求函数
时,求函数 的最大值及取得最大值时的
的最大值及取得最大值时的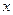 的值.
的值.