(本题15分)已知数列 中,
中, ,且
,且 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)求证:对一切 ,有
,有 .
.
(本小题满分12分)
已知定义在正实数集上的函数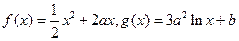 ,其中
,其中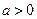 。设两曲线
。设两曲线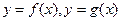 有公共点,且在公共点处的切线相同。
有公共点,且在公共点处的切线相同。
(1)若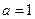 ,求
,求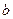 的值;(2)用
的值;(2)用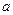 表示
表示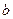 ,并求
,并求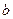 的最大值。
的最大值。
(本小题满分12分)
甲乙两个奥运会主办城市之间有7条网线并联,这7条网线能通过的信息量分别为l,1,2,2,2,3,3,现从中任选三条网线,设可通过的信息量为X,当可通过的信息量X≥6,则可保证信息通畅.
(1)求线路信息通畅的概率;
(2)求线路可通过的信息量X的分布列及期望。
(本小题满分12分)
如图,四棱锥P—ABCD中,ABCD为矩形,△PAD为等腰直角三角形,∠APD=90°,面PAD⊥面ABCD,且AB=1,AD=2,E、F分别为PC和BD的中点,
(1)证明:EF∥面PAD;
(2)证明:面PDC⊥面PAD;
(3)求锐二面角B—PD—C的余弦值.

(本小题满分12分)
设向量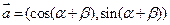 ,
,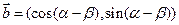 ,且
,且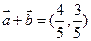 .
.
(1)求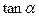 ;
;
(2)求 .
.
(本小题满分14分)
已知椭圆的左右焦点分别为 ,
, ,离心率为
,离心率为 ,Q是椭圆外动点,且
,Q是椭圆外动点,且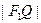 等于椭圆长轴的长,点P是线段
等于椭圆长轴的长,点P是线段 与椭圆的交点,点T是线段
与椭圆的交点,点T是线段 上异于
上异于 的一点,且
的一点,且 。
。
(1)求椭圆的方程;
(2)设直线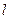 经过
经过 与椭圆交于M,N两点,
与椭圆交于M,N两点,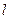 斜率为k,若
斜率为k,若 为钝角,求k的取值范围。
为钝角,求k的取值范围。