（本小题满分12分）已知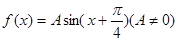
（1）若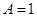
,将
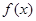的图像上各点的纵坐标不变，横坐标缩短为原来的2倍，再将所得图像上各点的横坐标不变，纵坐标扩大为原来的
倍，得到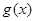
的图像，求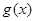的解析式及对称轴方程；
（2）若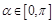
,
， 
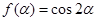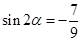，求
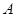的值．
(12分) 如图，已知△ABC是正三角形，EA、CD都垂直于平面ABC，且EA=AB=2a,DC=a,F是BE的中点，求证：(1) FD∥平面ABC; (2) AF⊥平面EDB.
(12分) 已知△ABC三边所在直线方程为AB：3x+4y+12=0，BC：4x－3y+16=0，CA：2x+y－2=0，求AC边上的高所在的直线方程.
已知函数f(x)=log2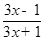
，(x∈(－∞，－
)∪(，+∞))
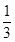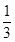（1）判断函数f(x)的奇偶性，并说明理由；
（2）判断函数f(x)在区间(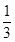，+∞)上的单调性．
经测试，光线每通过一块特殊的玻璃板，其强度将损失10%，已知原来的光线强度为a，设通过x块这样的玻璃板后的光线强度为y．
(1) 试写出y与x的函数关系式；
(2) 通过多少块玻璃板后，光线强度削弱到原来的
以下？
已知函数y＝f(x)是R上的偶函数，且x≥0时，f(x)＝(
)x－1．
（1）求f(x)的解析式；
（2）画出此函数的图象．