已知一条抛物线和一个椭圆都经过点M(1,2),它们在x轴上具有相同的焦点F1,且两者的对称轴都是坐标轴,抛物线的顶点在坐标原点。
(1)抛物线的方程和椭圆方程;
(2)设椭圆的另一个焦点是F2,经过F2的直线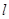 与抛物线交于P,Q两点,且满足
与抛物线交于P,Q两点,且满足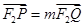 ,求m的取值范围。
,求m的取值范围。
(本小题满分12分)
设椭圆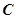 :
: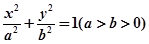 的左、右焦点分别为
的左、右焦点分别为 ,上顶点为
,上顶点为 ,过点
,过点 与
与 垂直的直线交
垂直的直线交 轴负半轴于点
轴负半轴于点 ,且
,且 .
.
(1)求椭圆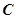 的离心率;
的离心率;
(2)若过 、
、 、
、 三点的圆恰好与直线
三点的圆恰好与直线 :
: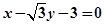 相切,求椭圆
相切,求椭圆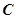 的
的
方程;
(3)在(2)的条件下,过右焦点 作斜率为
作斜率为 的直线
的直线 与椭圆
与椭圆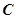 交于
交于 、
、 两
两
点,在 轴上是否存在点
轴上是否存在点 使得以
使得以 为邻边的平行四边形是菱形,
为邻边的平行四边形是菱形,
如果存在,求出 的取值范围,如果不存在,说明理由.
的取值范围,如果不存在,说明理由.
(本小题满分12分)
甲乙两名射手互不影响地进行射击训练,根据以往的数据统计,他们设计成绩的分布列如下:
| 射手甲 |
射手乙 |
||||||
| 环数 |
8 |
9 |
10 |
环数 |
8 |
9 |
10 |
| 概率 |
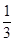 |
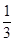 |
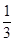 |
概率 |
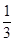 |
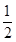 |
 |
(Ⅰ)若甲乙两射手各射击两次,求四次射击中恰有三次命中10环的概率;
(Ⅱ)若两个射手各射击1次,记所得的环数之和为 ,求
,求 的分布列和期望.
的分布列和期望.
(本小题满分12分)
如图(1)在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别是PC、PD、BC的中点,现将△PDC沿CD折起,使平面PDC⊥平面ABCD(如图2)
(1)求二面角G-EF-D的大小;
(2)在线段PB上确定一点Q,使PC⊥平面ADQ,并给出证明过程.
(本小题满分12分)
在△ABC中,角A、B、C所对的边分别为a、b、c,已知 ,
, ,
, .
.
(I)求c及△ABC的面积S;
(II)求 .
.
从某地成年男子中随机抽取n人,测得平均身高 =172cm,标准差sx=7.6cm,平均体重
=172cm,标准差sx=7.6cm,平均体重 =72kg,标准差sy=15.2kg,相关系数 r=
=72kg,标准差sy=15.2kg,相关系数 r= =0.5.求由身高估计平均体重的回归方程
=0.5.求由身高估计平均体重的回归方程 =a+bx,以及由体重估计平均身高的回归方程
=a+bx,以及由体重估计平均身高的回归方程 =c+dy.
=c+dy.