(本小题满分10分)求值:
(1)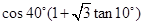
(2)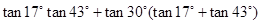
(本题满分16分)
已知函数
(Ⅰ)若函数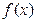 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数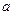 的最小值;
的最小值;
(Ⅱ)在函数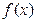 的图象上是否存在不同两点
的图象上是否存在不同两点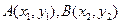 ,线段
,线段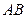 的中点的横坐标为
的中点的横坐标为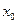 ,直线
,直线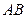 的斜率为
的斜率为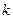 ,有
,有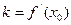 成立?若存在,请求出
成立?若存在,请求出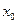 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
.(本题满分14分)
已知直线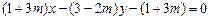
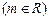 所经过的定点
所经过的定点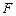 恰好是椭圆
恰好是椭圆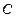 的一个焦点,且椭圆
的一个焦点,且椭圆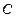 上的点到点
上的点到点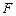 的最大距离为3.
的最大距离为3.
(Ⅰ) 求椭圆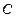 的标准方程;
的标准方程;
(Ⅱ) 设过点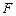 的直线
的直线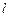 交椭圆于
交椭圆于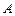 、
、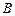 两点,若
两点,若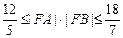 ,求直线
,求直线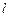 的斜率的取值范围.
的斜率的取值范围.
(本题满分14分)
如图1,在平面内,ABCD是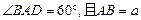 的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).
的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).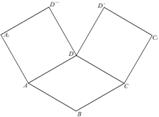

(Ⅰ) 设二面角E – AC – D1的大小为q,若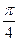 £q£
£q£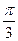 ,求线段BE长的取值范围;
,求线段BE长的取值范围;
(Ⅱ)在线段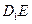 上存在点
上存在点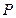 ,使平面
,使平面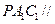 平面
平面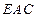 ,求
,求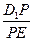 与BE之间满足的关系式,并证明:当0 < BE < a时,恒有
与BE之间满足的关系式,并证明:当0 < BE < a时,恒有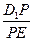 < 1.
< 1.
(本题满分14分)
已知正项数列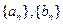 满足:对任意正整数
满足:对任意正整数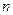 ,都有
,都有 成等差数列,
成等差数列,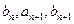 成等比数列,且
成等比数列,且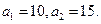
(Ⅰ)求证:数列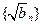 是等差数列;
是等差数列;
(Ⅱ)求数列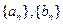 的通项公式;
的通项公式;
(Ⅲ) 设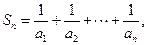 如果对任意正整数
如果对任意正整数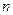 ,不等式
,不等式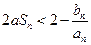 恒成立,求实数
恒成立,求实数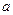 的取值范围.
的取值范围.
(本题满分14分)
已知函数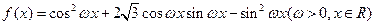 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为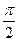 .
.
(Ⅰ)求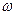 的值;
的值;
(Ⅱ)在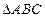 中,
中,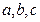 分别是角
分别是角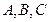 的对边,若
的对边,若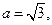
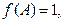 求
求 的最大值.
的最大值.