(本小题满分12分)设数列 满足
满足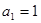 ,
,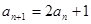
(1)求 的通项公式;
的通项公式;
(2)记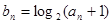 ,求数列
,求数列 的前
的前 项和为
项和为 .
.
把4个球随机地投入4个盒子中去,设ξ表示空盒子的个数,求ξ的分布列.
已知男人中有5%患色盲,女人中有0.25%患色盲,从100个男人和100个女人中任选一人.
(1)求此人患色盲的概率;
(2)如果此人是色盲,求此人是男人的概率.
袋中装有一些大小相同的球,其中有号数为1的球1个,号数为2的球2个,号数为3的球3个,…,号数为n的球n个.从袋中任取一球,其号数作为随机变量ξ,求ξ的概率分布和期望.
人寿保险中(某一年龄段),在一年的保险期内,每个被保险人需交纳保费a元,被保险人意外死亡则保险公司赔付3万元,出现非意外死亡则赔付1万元。经统计此年龄段一年内意外死亡的概率是p1,非意外死亡的概率为p2,则a需满足什么条件,保险公司才可能盈利.
一台设备由三大部件组成,在设备运转中,各部件需要调整的概率相应为0.10,0.20和0.30.假设各部件的状态相互独立,以ξ表示同时需要调整的部件数,试求ξ的数学期望Eξ和方差Dξ.