已知复数
．
（Ⅰ）若
为纯虚数，求实数
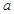的值；
（Ⅱ）若在复平面上对应的点在直线
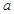上，求实数的值．
(12分)已知
是二次函数，不等式
的解集是
且在区间
上的最大值是12.
（1）求的解析式；
（2）是否存在实数
使得方程
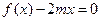在区间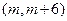
内有且只有两个不等的
实数根？若存在，求出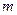
的取值范围；若不存在，说明理由.
(12分) 设向量
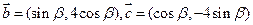
（1）若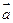
与
垂直，求
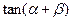的值；
（2）求
的最大值; （3）若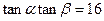
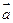，判断和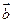
是平行还是垂直.
（本小题满分14分）
已知函数
，
；
（Ⅰ）证明
是奇函数；
（Ⅱ）证明在（-∞，-1）上单调递增；
（Ⅲ）分别计算
和
的值，由此概括出涉及函数和
的对所有不等于零的实数
都成立的一个等式，并加以证明
（本小题满分12分）
某开发商对去年市场上一种商品销售数量及销售利润情况进行了调查，发现：
①销售数量y1（万件）与时间（月份）具有满足下表的一次函数关系：
| 时间x（月份） |
1 |
2 |
3 |
… |
11 |
12 |
| 销售数量y1（万件） |
1.7 |
1.8 |
1.9 |
… |
2.7 |
2.8 |
②每一件的销售利润y2与时间x（月份）具有如下图所示的关系。
请根据以上信息解答下列问题：
(Ⅰ)在三月份，销售这种商品可获利润多少万元？
(Ⅱ)哪一个月的销售利润最大？请说明理由。
（本小题满分12分）
函数
的图象关于
对称，当
时
；
（Ⅰ）写出的解析式并作出图象；
（Ⅱ）根据图象讨论
（
）的根的情况.