为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数次测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.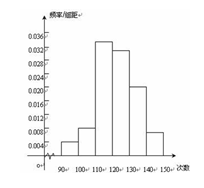
(1)第二小组的频率是多少?样本容量是多少?
(2)若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少?
(3)在这次测试中,学生跳绳次数的中位数落在哪个小组内?请说明理由。
直线x+m2y+6=0与直线(m-2)x+3my+2m=0没有公共点,求实数m的值.
①求平行于直线3x+4y-12=0,且与它的距离是7的直线的方程;
②求垂直于直线x+3y-5="0," 且与点P(-1,0)的距离是 的直线的方程.
的直线的方程.
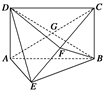
如图所示,矩形 中,
中,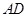 ⊥平面
⊥平面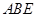 ,
,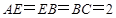 ,
, 为
为 上的点,且
上的点,且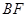 ⊥平面
⊥平面 .
.
(1)求证: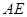 ⊥平面
⊥平面 ;
;
(2)求三棱锥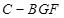 的体积.
的体积.
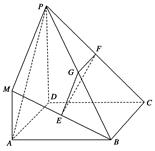
在如图所示的几何体中,四边形 是正方形,
是正方形, ⊥平面
⊥平面 ,
, ∥
∥ ,
,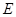 、
、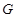 、
、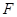 分别为
分别为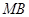 、
、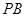 、
、 的中点,且
的中点,且 .
.
(1)求证:平面 ⊥平面
⊥平面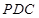 ;
;
(2)求三棱锥 与四棱锥
与四棱锥 的体积之比.
的体积之比.
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图中的侧(左)视图、俯视图,在直观图中, 是
是 的中点,侧(左)视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点,侧(左)视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(1)求出该几何体的体积;
(2)若 是
是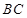 的中点,求证:
的中点,求证: ∥平面
∥平面 ;
;
(3)求证:平面 ⊥平面
⊥平面 .
.