已知 为椭圆
为椭圆 的左右焦点,点
的左右焦点,点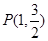 为其上一点,且有
为其上一点,且有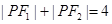
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)过 的直线
的直线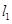 与椭圆
与椭圆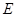 交于
交于 两点,过
两点,过 与
与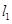 平行的直线
平行的直线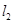 与椭圆
与椭圆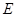 交于
交于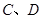 两点,求四边形
两点,求四边形 的面积
的面积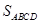 的最大值.
的最大值.
(本小题满分12分)如图,在平面直角坐标系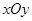 中,以
中,以 轴为始边做两个锐角
轴为始边做两个锐角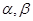 ,它们的终边分别与单位圆相交于A、B两点,已知A、B的横坐标分别为
,它们的终边分别与单位圆相交于A、B两点,已知A、B的横坐标分别为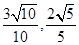 .
.
(1)求 的值; (2)求
的值; (2)求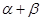 的值.
的值.
(本小题满分10分)已知 ,
,
(1)求 的夹角
的夹角 ;(2)求
;(2)求 的值.
的值.
(本小题满分12分)已知数列 .
.
(1)求数列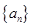 的通项公式;
的通项公式;
(2)设 ,探求使
,探求使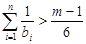 恒成立的
恒成立的 的最大整数值.
的最大整数值.
(本小题满分12分)
港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站为31海里,该轮船从B处沿正西方向航行20海里后到达D处观测站,已知观测站与检查站距离21海里,问检查站C离港口A有多远?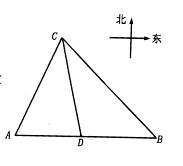
(本小题满分12分)
如图,平面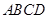 ⊥平面
⊥平面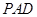 ,
,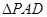 是直角三角形,
是直角三角形,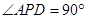 ,四边形
,四边形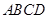 是直角梯形,其中
是直角梯形,其中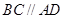 ,
,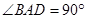 ,
,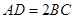 ,且
,且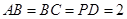 ,
,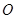 是
是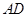 的中点,
的中点,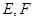 分别是
分别是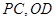 的中点.
的中点. 
(Ⅰ)求证: 平面
平面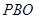 ;
;
(Ⅱ)求二面角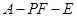 的正切值.
的正切值.