如图3,在直三棱柱ABC—A1B1C1中,AB1⊥BC1,AB=CC1=1,BC=2.
(1)求证:A1C1⊥AB;
(2)求点B1到平面ABC1的距离.
如图,在棱长为a的正方体ABCD—A1B1C1D1中,M、N分别是AA1、D1C1的中点,过D、M、N三点的平面与正方体的下底面相交于直线l;
(1)画出直线l;
(2)设l∩A1B1=P,求PB1的长;
(3)求D到l的距离.
已知圆C:(x-1)2+y2=9内有一点P(2,2),过点P作直线l交圆C于A、B两点.
(1)当l经过圆心C时,求直线l的方程;
(2)当弦AB被点P平分时,写出直线l的方程;
(3)当直线l的倾斜角为45°时,求弦AB的长.
已知⊙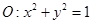 和点
和点 .
.
(Ⅰ)过点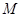 向⊙
向⊙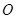 引切线
引切线 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)求以点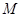 为圆心,且被直线
为圆心,且被直线 截得的弦长为4的⊙
截得的弦长为4的⊙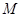 的方程;
的方程;
(Ⅲ)设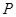 为(Ⅱ)中⊙
为(Ⅱ)中⊙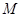 上任一点,过点
上任一点,过点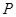 向⊙
向⊙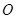 引切线,切点为
引切线,切点为 . 试探究:平面内是否存在一定点
. 试探究:平面内是否存在一定点 ,使得
,使得 为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
已知数列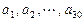 ,其中
,其中 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;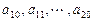 是公差为
是公差为 的等差数列;
的等差数列;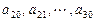 是公差为
是公差为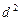 的等差数列(
的等差数列(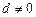 ).
).
(1)若 ,求
,求 ;
;
(2)试写出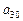 关于
关于 的关系式,并求
的关系式,并求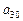 的取值范围;
的取值范围;
(3)续写已知数列,使得 是公差为
是公差为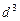 的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?