已知抛物线与
轴交于A（1，0），B（－3，0）两点，与
轴交于点C（0，3），抛物线顶点P，连接AC。
（1）求抛物的解析式；
（2）在抛物线上找一点D，使得DC与AC垂直，且直线DC与轴交于点Q，求点D的坐标。
（3）在抛物线的对称轴上，是否存在一点M，使得S△MAP=2S△ACP，若存在，求出M点的坐标，若不存在，请说明理由。
计算：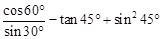
。
解方程：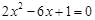
。
A（1，0），B（3，0
）。
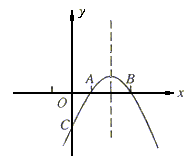
（1）求抛物线的解析式；
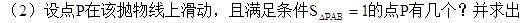
所有点P的坐标；（3）设抛物线交y轴于点C，问该抛物线对称轴上是否存在点M，使得△MAC的周长最小。若存在，求出点M的
坐标；若不存在，请说明理由。
如图所示，矩形ABCD，AB＞AD，E在AD上，将△ABE沿BE折叠后，A点正好落在CD上的点F。
（1）用尺规作出E、F；
（2）若AE＝5，DE＝3，求折痕BE的长；
（3）试判断四边形ABFE是否一定有内切圆。
有研究发现，人体
在注射一定剂量的某种药物后的数小时内，体内血液中的药物浓度（即血药浓度）y毫克/升是时间t（小时）的二次函数，已知某病人的三次化验结果如下
表：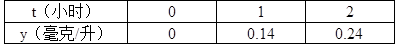
（1）求y与t的函数关系式；
（2）在注射后的第几小时，该病人体内的血药浓度达到最大？最大浓度是多少？
（3）该病人在注射后的几个小时内，体内的血药浓度超过0.3毫克/升？