在平面直角坐标系xoy中,给出如下定义:形如y=a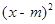 +a(x-m)与y=a
+a(x-m)与y=a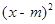 -a(x-m)的两个二次函数的图象叫做“兄弟抛物线”.
-a(x-m)的两个二次函数的图象叫做“兄弟抛物线”.
(1)试写出一对兄弟抛物线的解析式 与 ;
(2)判断二次函数y=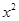 -x与y=
-x与y=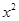 -3x+2的图象是否为兄弟抛物线,如果是,求出a与m的值,如果不是,请说明理由;
-3x+2的图象是否为兄弟抛物线,如果是,求出a与m的值,如果不是,请说明理由;
(3)若一对兄弟抛物线各自与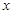 轴的两个交点和其顶点构成直角三角形,其中一个抛物线的对称轴为直线x=2且开口向上,请直接写出这对兄弟抛物线的解析式.
轴的两个交点和其顶点构成直角三角形,其中一个抛物线的对称轴为直线x=2且开口向上,请直接写出这对兄弟抛物线的解析式.
如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm。
(1)若P、Q是△ABC边上的两个动点,其中点P从A沿A→B方向运动,速度为每秒1cm,点Q从B沿B→C方向运动,速度为每秒2cm,两点同时出发,设出发时间为t秒.①当t=1秒时,求PQ的长;②从出发几秒钟后,△PQB是等腰三角形?
(2)若M在△ABC边上沿B→A→C方向以每秒3cm的速度运动,则当点M在边CA上运动时,求△BCM成为等腰三角形时M运动的时间.
两根电线杆AB、CD,AB=5m,CD=3m,它们的底部相距8m,现在要在两根电线杆底端之间(线段BD上)选一点E,由E分别向两根电线杆顶端拉钢索AE、CE.若使钢索AE与CE相等,那么点E应该选在距点B多少米处?
如图,长方形纸片ABCD,AD∥BC,将长方形纸片折叠,使点D与点B重合,点C落在点C'处,折痕为EF,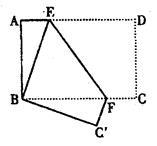
(1)求证:BE=BF.
(2)若∠ABE=18°,求∠BFE的度数.
(3)若AB=6,AD=8,求AE的长.
已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为AB边上一点.
求证:(1)BD=AE.
(2)若线段AD=5,AB=17,求线段ED的长。
如图,∠DCE=90°,CD=CE,AD⊥AC,BE⊥AC,垂足分别为A、B.试说明AD+AB=BE.