(本小题满分12分)将一个半径适当的小球放入如图所示的容器最上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物 次,最后落入
次,最后落入 袋或
袋或 袋中.已知小球每次遇到障碍物时,向左、右两边下落的概率分别是
袋中.已知小球每次遇到障碍物时,向左、右两边下落的概率分别是

(1)分别求出小球落入 袋和
袋和 袋中的概率;
袋中的概率;
(2)在容器的入口处依次放入 个小球,记
个小球,记 为落入
为落入 袋中的小球个数,求
袋中的小球个数,求 的分布列和数学期望.
的分布列和数学期望.
已知函数 .
.
(1)当 时,求不等式
时,求不等式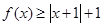 的解集;
的解集;
(2)若不等式 存在实数解,求实数
存在实数解,求实数 的取值范围.
的取值范围.
在平面直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为 ,(其中
,(其中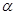 为参数,
为参数,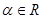 ),在极坐标系(以坐标原点
),在极坐标系(以坐标原点 为极点,以
为极点,以 轴非负半轴为极轴)中,曲线
轴非负半轴为极轴)中,曲线 的极坐标方程为
的极坐标方程为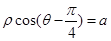 .
.
(1)把曲线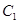 和
和 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(2)若曲线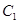 上恰有三个点到曲线
上恰有三个点到曲线 的距离为
的距离为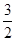 ,求曲线
,求曲线 的直角坐标方程.
的直角坐标方程.
如图,半圆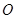 的直径
的直径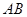 的长为4,点
的长为4,点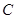 平分弧
平分弧 ,过
,过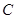 作
作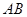 的垂线交
的垂线交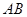 于
于 ,交
,交 于
于 .
.
(1)求证: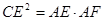 :
:
(2)若 是
是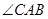 的角平分线,求
的角平分线,求 的长.
的长.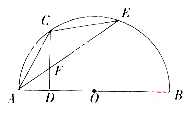
用总长为14.8m的钢条制作一个长方体容器的框架,如果所制作容器的底面的一边比另一边长0.5m,那么高为多少时容器的容积最大?并求出它的最大容积.
在 中,内角
中,内角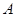 ,
,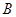 ,
, 所对的边分别为
所对的边分别为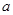 ,
, ,
, ,已知
,已知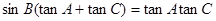 .
.
(1)求证: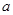 ,
, ,
, 成等比数列;
成等比数列;
(2)若 ,
,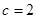 ,求
,求 的面积
的面积 .
.