(本题8分)如图,在△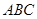 中,
中,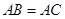 ,点
,点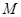 在
在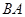 的延长线上.
的延长线上.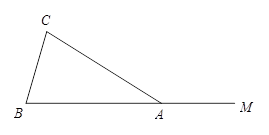
(1)按下列要求作图,并在图中标明相应的字母.
①作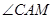 的平分线
的平分线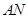 ;
;
②作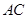 的中点
的中点 ,连接
,连接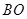 ,并延长
,并延长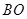 交
交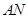 于点
于点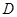 ,连接
,连接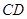 .
.
(2)在(1)的条件下,判断四边形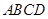 的形状.并证明你的结论.
的形状.并证明你的结论.
把下列各实数填在相应的大括号内 ,-|-3|,
,-|-3|, ,0,
,0,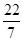 ,-3.
,-3.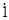 ,
,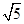 ,1-
,1- , 1.1010010001…(两个1之间依次多1个0)
, 1.1010010001…(两个1之间依次多1个0)
整数{ …};
分数{ …};
无理数{ …};
画出数轴,把下列各数:-5、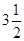 、0、
、0、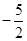 在数轴上表示出来,并用“<”号从小到大连接.
在数轴上表示出来,并用“<”号从小到大连接.
如图,学校准备新建一个长度为L的读书长廊,并准备用若干块带有花纹和没有花纹的两种规格大小相同的正方形地面砖搭配在一起,按图中所示的规律拼成图案铺满长廊,已知每个小正方形地面砖的边长均为0.5m.
(1)按图示规律,第一图案的长度L1=m;第二个图案的长度L2= m;
(2)用代数式表示带有花纹的地面砖块数n与走廊的长度Ln(m)之间的关系 ;
如图,抛物线y=ax2+bx+c经过A(﹣3.0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.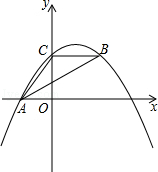
(1)求抛物线的解析式;
(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.
如图,△ABC是边长为4cm的等边三角形,AD为BC边上的高,点P沿BC向终点C运动,速度为1cm/s,点Q沿CA、AB向终点B运动,速度为2cm/s,若点P、Q两点同时出发,设它们的运动时间为x(s).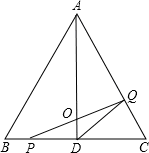
(l)求x为何值时,PQ⊥AC;x为何值时,PQ⊥AB?
(2)当O<x<2时,AD是否能平分△PQD的面积?若能,说出理由;
(3)探索以PQ为直径的圆与AC的位置关系,请写出相应位置关系的x的取值范围(不要求写出过程).