如图,抛物线y=ax2+bx+c经过A(﹣3.0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.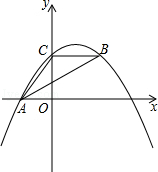
(1)求抛物线的解析式;
(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.
小兰和小颖用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形,转动两个转盘各一次,若两次指针所指数字之和小于4,则小兰胜,否则小颖胜(指针指在分界线时重转),这个游戏对双方公平吗?请用树状图或列表法说明理由.

一汽车从甲地出发开往相距240 km的乙地,出发后第一小时内按原计划的速度匀速行驶,1小时后比原来的速度加快 ,比原计划提前24 min到达乙地,求汽车出发后第1小时内的行驶速度.
在平面直角坐标系 xOy中,抛物线 y= ax 2+ bx+ c与 y轴交于点 C,其顶点记为 M,自变量 x=﹣1和 x=5对应的函数值相等.若点 M在直线 l: y=﹣12 x+16上,点(3,﹣4)在抛物线上.
(1)求该抛物线的解析式;
(2)设 y= ax 2+ bx+ c对称轴右侧 x轴上方的图象上任一点为 P,在 x轴上有一点 A(﹣ ,0),试比较锐角∠ PCO与∠ ACO的大小(不必证明),并写出相应的 P点横坐标 x的取值范围.
(3)直线 l与抛物线另一交点记为 B, Q为线段 BM上一动点(点 Q不与 M重合).设 Q点坐标为( t, n),过 Q作 QH⊥ x轴于点 H,将以点 Q, H, O, C为顶点的四边形的面积 S表示为 t的函数,标出自变量 t的取值范围,并求出 S可能取得的最大值.
如图,点 A, B, C, D是直径为 AB的⊙ O上的四个点, C是劣弧 的中点, AC与 BD交于点 E.
(1)求证: DC 2= CE• AC;
(2)若 AE=2, EC=1,求证:△ AOD是正三角形;
(3)在(2)的条件下,过点 C作⊙ O的切线,交 AB的延长线于点 H,求△ ACH的面积.

已知反比例函数 y= ( k为常数).
(1)若点 P 1( , y 1)和点 P 2(﹣ , y 2)是该反比例函数图象上的两点,试利用反比例函数的性质比较 y 1和 y 2的大小;
(2)设点 P( m, n)( m>0)是其图象上的一点,过点 P作 PM⊥ x轴于点 M.若tan∠ POM=2, PO= ( O为坐标原点),求 k的值,并直接写出不等式 kx+ >0的解集.