如图，△ABC是边长为4cm的等边三角形，AD为BC边上的高-优题课

如图，△ABC是边长为4cm的等边三角形，AD为BC边上的高，点P沿BC向终点C运动，速度为1cm/s，点Q沿CA、AB向终点B运动，速度为2cm/s，若点P、Q两点同时出发，设它们的运动时间为x（s）．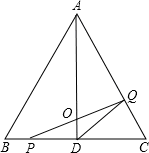

（l）求x为何值时，PQ⊥AC；x为何值时，PQ⊥AB？
（2）当O＜x＜2时，AD是否能平分△PQD的面积？若能，说出理由；
（3）探索以PQ为直径的圆与AC的位置关系，请写出相应位置关系的x的取值范围（不要求写出过程）．

科目数学题型解答题难度中等

知识点：三角形的五心圆幂定理

如图， $O ， R$ 是同一水平线上的两点，无人机从 $O$ 点竖直上升到 $A$ 点时，测得 $A$ 到 $R$ 点的距离为 $40 m$ ， $R$ 点的俯角为 $24.2 °$ ，无人机继续竖直上升到 $B$ 点，测得 $R$ 点的俯角为 $36.9 °$ ．求无人机从 $A$ 点到 $B$ 点的上升高度 $A B$ （精确到 $0.1 m$ ）．

参考数据： $\sin 24.2 ° \approx 0.41 ， \cos 24.2 ° \approx 0.91 ， \tan 24.2 ° \approx 0.45 ， \sin 36.9 ° \approx 0.60 ， \cos 36.9 ° \approx 0.80 ， \tan 36.9 ° \approx 0.75$ ．

【观察思考】

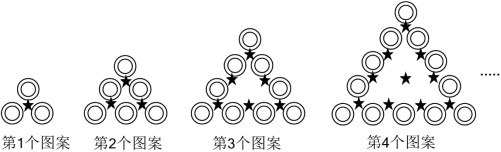
【规律发现】

请用含 $n$ 的式子填空：

（1）第 $n$ 个图案中“◎”的个数为＿＿＿＿＿；

（2）第1个图案中“★”的个数可表示为 $\frac{1 \times 2}{2}$ ，第 $2$ 个图案中“★”的个数可表示为 $\frac{2 \times 3}{2}$ ，第 $3$ 个图案中“★”的个数可表示为 $\frac{3 \times 4}{2}$ ，第 $4$ 个图案中“★”的个数可表示为 $\frac{4 \times 5}{2}$ ，……，第 $n$ 个图案中“★”的个数可表示为＿＿＿＿＿．

【规律应用】

（3）结合图案中“★”的排列方式及上述规律，求正整数 $n$ ，使得连续的正整数之和 $1 + 2 + 3 + \dots \dots + n$ 等于第 $n$ 个图案中“◎”的个数的 $2$ 倍．

根据经营情况，公司对某商品在甲、乙两地的销售单价进行了如下调整：甲地上涨 $10 %$ ，乙地降价 $5$ 元．已知销售单价调整前甲地比乙地少 $10$ 元，调整后甲地比乙地少 $1$ 元，求调整前甲、乙两地该商品的销售单价．

先化简，再求值： $\frac{x^{2} + 2 x + 1}{x + 1}$ ，其中 $x ＝ \sqrt{2} - 1$ ．

综合运用

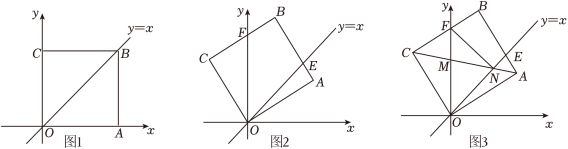
如图1，在平面直角坐标系中，正方形 $O A B C$ 的顶点 $A$ 在 $x$ 轴的正半轴上．如图2，将正方形 $O A B C$ 绕点 $O$ 逆时针旋转，旋转角为 $α （ 0 ° ＜ α ＜ 45 ° ）$ ， $A B$ 交直线 $y ＝ x$ 于点 $E$ ， $B C$ 交 $y$ 轴于点 $F$ ．

（1）当旋转角 $∠ C O F$ 为多少度时， $O E ＝ O F$ ；（直接写出结果，不要求写解答过程）

（2）若点 $A （ 4 ， 3 ）$ ，求 $F C$ 的长；

（3）如图3，对角线 $A C$ 交 $y$ 轴于点 $M$ ，交直线 $y ＝ x$ 于点 $N$ ，连接 $F N$ ．将 $△ O F N$ 与 $△ O C F$ 的面积分别记为 $S_{1}$ 与 $S_{2}$ ．设 $S ＝ S_{1} ﹣ S_{2}$ ， $A N ＝ n$ ，求 $S$ 关于 $n$ 的函数表达式．

试卷网试题网古诗词网作文网范文网