(10 分)我市某风景区门票价格如图所示黄冈赤壁旅游公司有甲、乙两个旅行团队,计划在“五一”小黄金周期间到该景点游玩,两团队游客人数之和为120 人,乙团队人数不超过50 人.设甲团队人数为x 人,如果甲、乙两团队分别购买门票,两团队门票款之和为W 元.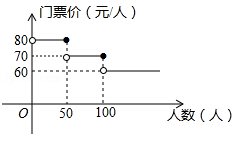
(1)求W 关于x 的函数关系式,并写出自变量x 的取值范围;
(2)若甲团队人数不超过100 人,请说明甲、乙两团队联合购票比分别购票最多可节约多少钱;
(3)“五一”小黄金周之后,该风景区对门票价格作了如下调整:人数不超过50 人时,门票价格不变;人数超过50 人但不超过100 人时,每张门票降价a 元;人数超过100 人时,每张门票降价2a 元.在(2)的条件下,若甲、乙两个旅行团队“五一”小黄金周之后去游玩,最多可节约3400 元,求a 的值.
如图,抛物线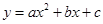 与
与 轴交于
轴交于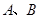 两点,与
两点,与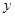 轴相交于点
轴相交于点 .连结AC、BC,B、C两点的坐标分别为B(1,0)、
.连结AC、BC,B、C两点的坐标分别为B(1,0)、 ,且当x=-10和x=8时函数的值
,且当x=-10和x=8时函数的值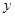 相等.
相等.求a、b、c的值;
若点
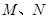 同时从
同时从 点出发,均以每秒1个单位长度的速度分别沿
点出发,均以每秒1个单位长度的速度分别沿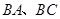 边运动,其中一个点到达终点时,另一点也随之停止运动.连结
边运动,其中一个点到达终点时,另一点也随之停止运动.连结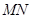 ,将
,将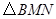 沿
沿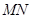 翻折,当运动时间为几秒时,
翻折,当运动时间为几秒时, 点恰好落在
点恰好落在 边上的
边上的 处?并求点
处?并求点 的坐标及四边形
的坐标及四边形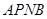 的面积;
的面积;上下平移该抛物线得到新的抛物线,设新抛物线的顶点为D,对称轴与x轴的交点为E,若△ODE与△OBC相似,求新抛物线的解析式。

有一种葡萄:从树上摘下后不保鲜最多只能存放一周,如果放在冷藏室,可以延长保鲜时间,但每天仍有一定数量的葡萄变质,假设保鲜期内的重量基本保持不变,现有一位个体户,按市场价收购了这种葡萄200千克放在冷藏室内,此时市场价为每千克2元,据测算,此后每千克鲜葡萄的市场价格每天可以上涨0.2元,但是,存放一天需各种费用20元,平均每天还有1千克葡萄变质丢弃.存放x天后将鲜葡萄一次性出售,设鲜葡萄的销售金额为Y元,写出Y关于x的函数关系式;
为了使鲜葡萄的销售金额为760元,又为了尽早清空冷藏室,则需要在几天后一次性出售完;
问个体户将这批葡萄存放多少天后一次性出售,可获得最大利润?最大利润是多少?(本题不要求写出自变量x的取值范围)
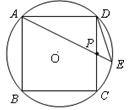
如图,已知:边长为1的正方形ABCD内接于⊙O,P为边CD的中点,直线AP交圆于E点.求弦DE的长;
若Q是线段BC上一动点,当CQ长为何值时,三角形ADP与以Q,C,P为顶点的三角形相似。
某文印店,一次性复印收费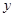 (元)与复印面数(8开纸)
(元)与复印面数(8开纸) (面)的函数关系如图2—8所示:
(面)的函数关系如图2—8所示:从图象中可看出:复印超过50面的部分每面收费元,复印200面平均每面收费元;
两同学各需要复印都不多于50面的资料,他们合起来去该店复印,结果比各自独去复印两人共节省2元钱,问其中一位同学所需复印的面数不能少于多少面?

某校为积极开展人防教育,抽取了部分八年级的学生举行人防知识竞赛,并将竞赛成绩整理后作出如下的统计图。已知从左至右第一、二组的频率和是0.12,第二、三、四组的频数比是4:17:15,成绩不小于100分的同学占96%。结合统计图回答下列问题:从左至右第一组的频率是多少?共有多少人参加了这次人防知识竞赛?
成绩不小于130分的为优秀,若将原统计图改成扇形统计图,则优秀部分对应的圆心角应画成几度角?
如果这次竞赛成绩的中位数是120分,
那么成绩为120分的学生至少有多少人?