设正项数列{an}(n≥5)对任意正整数k(k≥3)恒满足: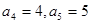 ,且
,且 .
.
(1)求数列{an}的通项公式;
(2)是否存在整数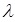 ,使得
,使得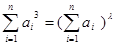 对于任意正整数n恒成立?若存在,求出
对于任意正整数n恒成立?若存在,求出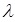 的值;若不存在,说明理由。(注:
的值;若不存在,说明理由。(注: )
)
如图,在四棱锥P-ABCD中,底面ABCD是矩形,M、N分别为PA、BC的中点, PD⊥平面ABCD,且PD=AD=
PD⊥平面ABCD,且PD=AD= ,CD=1
,CD=1
(1)证明:MN∥平面PCD;
(2)证明:MC⊥BD;
(3)求二面角A—PB—D的余弦值。
已知函数 .
.
(1)求 的最小正周期和图象的对称轴方程;
的最小正周期和图象的对称轴方程;
(2)求 在区间
在区间 上的最大值和最小值。
上的最大值和最小值。
设函数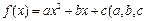 为实数,且
为实数,且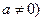 ,
,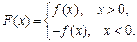
(Ⅰ)若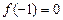 ,曲线
,曲线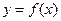 通过点
通过点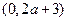 ,且在点
,且在点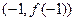 处的切线垂直于
处的切线垂直于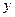 轴,求
轴,求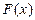 的表达式;
的表达式;
(Ⅱ)在(Ⅰ)在条件下,当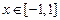 时,
时,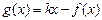 是单调函数,求实数
是单调函数,求实数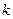 的取值范围;
的取值范围;
(Ⅲ)设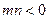 ,
,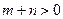 ,
,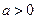 ,且
,且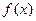 为偶函数,证明
为偶函数,证明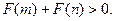
已知椭圆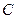 的中心在原点,一个焦点
的中心在原点,一个焦点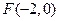 ,且长轴长与短轴长的比是
,且长轴长与短轴长的比是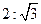 .
.
(Ⅰ)求椭圆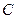 的方程;
的方程;
(Ⅱ)设点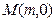 在椭圆
在椭圆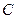 的长轴上,点
的长轴上,点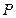 是椭圆上任意一点. 当
是椭圆上任意一点. 当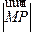 最小时,点
最小时,点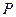 恰好落在椭圆的右顶点,求实数
恰好落在椭圆的右顶点,求实数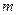 的取值范围.
的取值范围.
设数列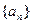 的前
的前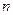 项和为
项和为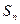 ,已知
,已知
(Ⅰ)求证:数列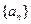 为等差数列,并写出
为等差数列,并写出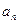 关于
关于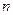 的表达式;
的表达式;
(Ⅱ)若数列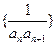 前
前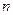 项和为
项和为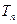 ,问满足
,问满足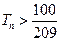 的最小正整数
的最小正整数 是多少? .
是多少? .