(本题15分)已知直线 的方程为
的方程为 ,
,
(1)若直线 的斜率是
的斜率是 ;求
;求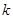 的值;
的值;
(2)若直线 在
在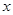 轴、
轴、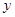 轴上的截距之和等于
轴上的截距之和等于 ;求
;求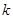 的值;
的值;
(3)求证:直线 恒过定点。
恒过定点。
已知函数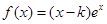 .
.
(1)求 的单调区间;
的单调区间;
(2)求 在区间
在区间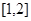 上的最小值;
上的最小值;
(3)设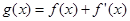 ,当
,当 时,对任意
时,对任意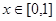 ,都有
,都有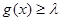 成立,求实数
成立,求实数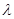 的取值范围。
的取值范围。
(本小题满分12分)
已知过点 的直线
的直线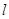 与抛物线
与抛物线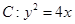 交于
交于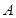 、
、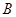 两点,
两点,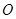 为坐标原点.
为坐标原点.
(1)若以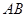 为直径的圆经过原点
为直径的圆经过原点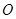 ,求直线
,求直线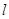 的方程;
的方程;
(2)若线段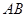 的中垂线交
的中垂线交 轴于点
轴于点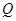 ,求
,求 面积的取
面积的取 值范围.
值范围.
.(本小题满分12分)
汽车在道路上行驶每100千米平均燃料消耗量(单位:升)称为百公里油耗.已知某型号汽车在匀速行驶中每小时的耗油量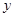 (升)关于行驶速度
(升)关于行驶速度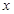 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: .
.
(1)当该型号汽车以40千米/小时的速度匀速行驶时,百公里油耗是多少升?
(2)当该型号汽车以多大的速度匀速行驶时,百公里油耗最低?最低为多少升?
若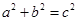 ,求证:
,求证: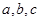 不可能都是奇数。
不可能都是奇数。
已知命题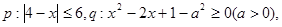 若非
若非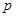 是
是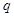 的充分不必要条件,求
的充分不必要条件,求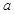 的取值范围。
的取值范围。