(本题15分)根据下列条件,求圆的方程
(1)求经过两点 ,且圆心在y轴上的圆的方程。
,且圆心在y轴上的圆的方程。
(2)圆的的半径为1,圆心与点(1,0)关于 对称的圆的方程。
对称的圆的方程。
设命题p:函数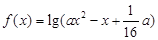 的定义域为R;命题q:不等式
的定义域为R;命题q:不等式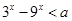 对任意
对任意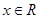 恒成立.
恒成立.
(Ⅰ)如果p是真命题,求实数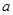 的取值范围;
的取值范围;
(Ⅱ)如果命题“p或q”为真命题且“p且q”为假命题,求实数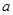 的取值范围.
的取值范围.
已知集合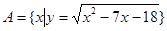 ,集合
,集合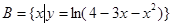 ,集合
,集合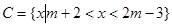 .
.
(Ⅰ)设全集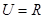 ,求
,求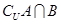 ;(Ⅱ)若
;(Ⅱ)若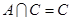 ,求实数
,求实数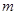 的取值范围.
的取值范围.
极坐标系中椭圆C的方程为 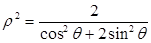
以极点为原点,极轴为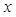 轴非负半轴,建立平面直角坐标 系,且两坐标系取相同的单位长度.
轴非负半轴,建立平面直角坐标 系,且两坐标系取相同的单位长度.
(Ⅰ)求该椭圆的直角标方程;若椭圆上任一点坐标为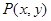 ,求
,求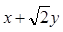 的取值范围;
的取值范围;
(Ⅱ)若椭圆的两条弦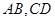 交于点
交于点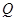 ,且直线
,且直线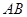 与
与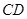 的倾斜角互补,
的倾斜角互补,
求证: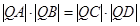 .
.
如图,设AB,CD为⊙O的两直径,过B作PB垂直于AB,并与CD延长线相交于点P,过P作直线与⊙O分别交于E,F两点,连结AE,AF分别与CD交于G、H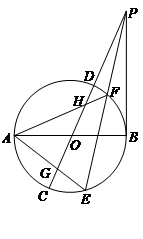
(Ⅰ)设EF中点为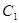 ,求证:O、
,求证:O、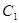 、B、P四点共圆
、B、P四点共圆
(Ⅱ)求证:OG =OH.
已知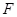 为抛物线
为抛物线 的焦点,抛物线上点
的焦点,抛物线上点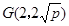 满足
满足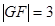
(Ⅰ)求抛物线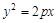 的方程;
的方程;
(Ⅱ)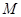 点的坐标为(
点的坐标为(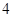 ,
, ),过点F作斜率为
),过点F作斜率为 的直线与抛物线交于
的直线与抛物线交于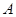 、
、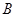 两点,
两点,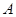 、
、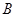 两点的横坐标均不为
两点的横坐标均不为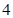 ,连结
,连结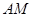 、
、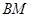 并延长交抛物线于
并延长交抛物线于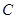 、
、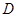 两点,设直线
两点,设直线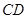 的斜率为
的斜率为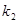 ,问
,问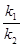 是否为定值,若是求出该定值,若不是说明理由.
是否为定值,若是求出该定值,若不是说明理由.